目录
向量与矩阵
关于向量与矩阵的概念就不多做介绍了,我们这里重点讨论向量与矩阵在OpenGL中的几何意义及应用。
一、向量
向量分为行向量与列向量

1.等式中使用列向量形式更好
2.线性代数书中使用列向量
3.多本计算机图形学都是使用的列向量
4.OpenGL 使⽤的是列向量
二、矩阵
1、是否能够相乘
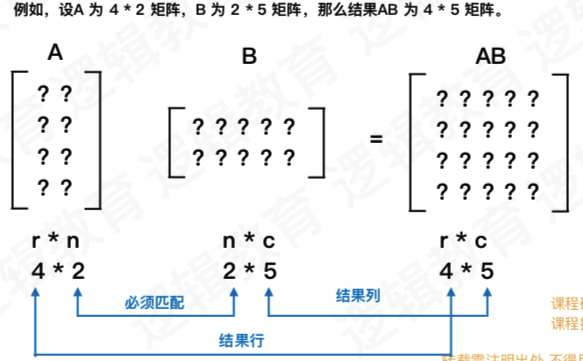
2、矩阵相乘计算
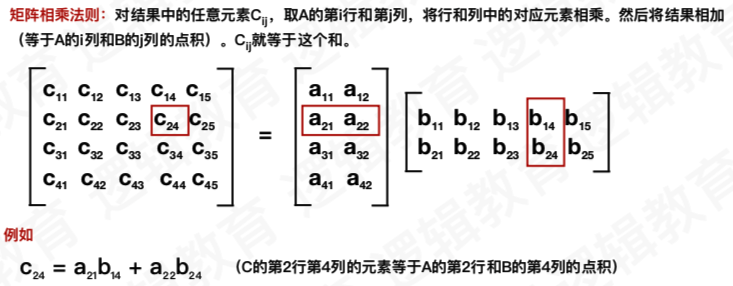
矩阵的几何意义
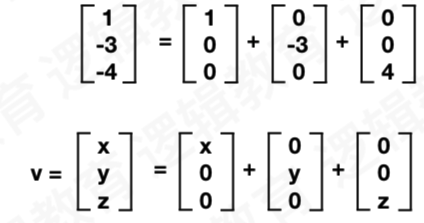
一、向量的位移
向量 [1,-3 -4] 是如果实现位移?
位移 [1,0,0], 随后位移[0,-3,0], 最后位移[0,0,4]
二、向量的旋转和缩放
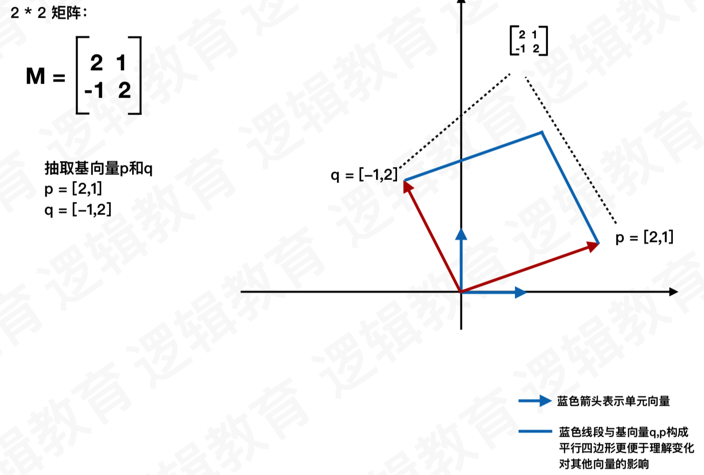
1、基向量
要想理解向量是如何通过矩阵进行变化的首先要理解基向量通过矩阵的变化。
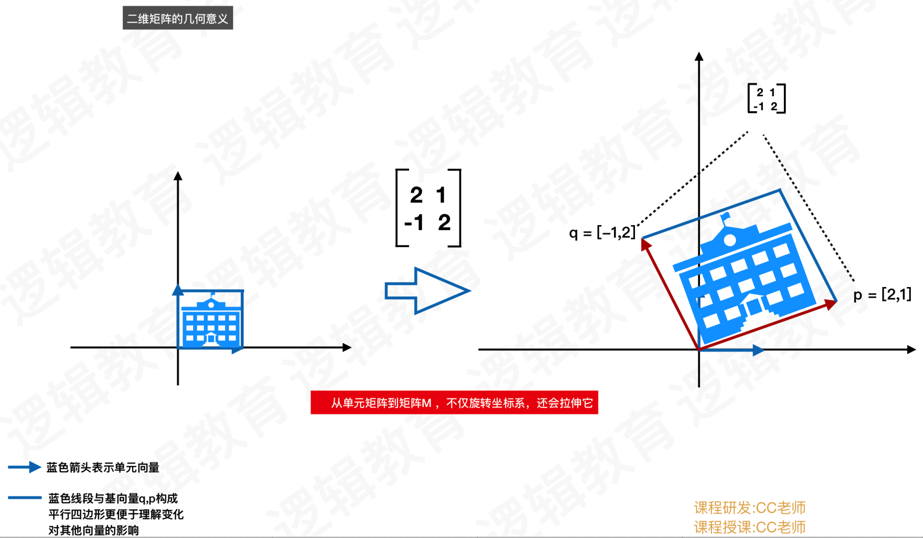
如果把矩阵的行解释为坐标的基向量,那么乘以该矩阵就是做了⼀次坐标转换。若aM = b,我们就可以说,M将a向量转换成了b向量。
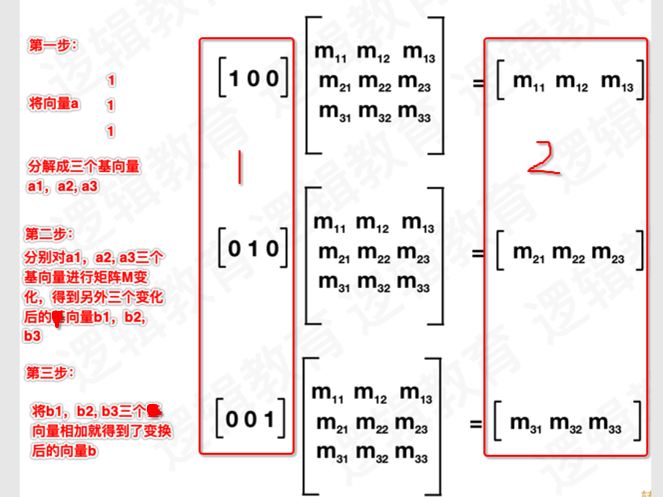
通过上图我们就将向量a,经过矩阵M转化为了向量b.
在OpenGL的物体坐标系中的顶点数据可以看成是一个一个的向量,对所有的向量进行矩阵M变化就可以对整个物体完成平移、缩放、旋转等操作。
2、二维矩阵的几何意义
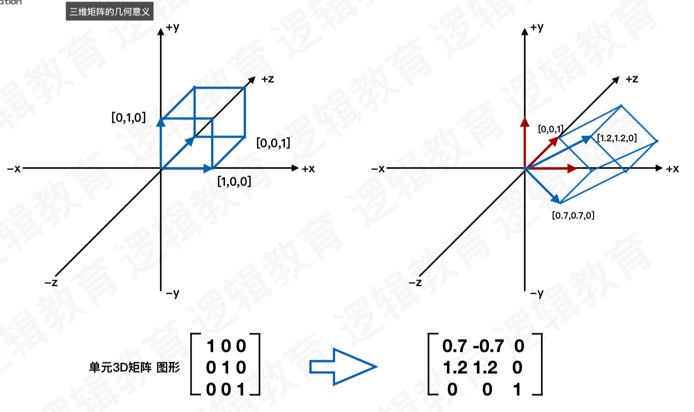
3、三维矩阵的几何意义
三、向量的旋转
矩阵M包含了旋转和缩放变化,单纯的旋转矩阵可以理解成是M的一个子集 (M旋转),(M旋转)它自身是有一些规律的。
1、2D旋转矩阵的构成
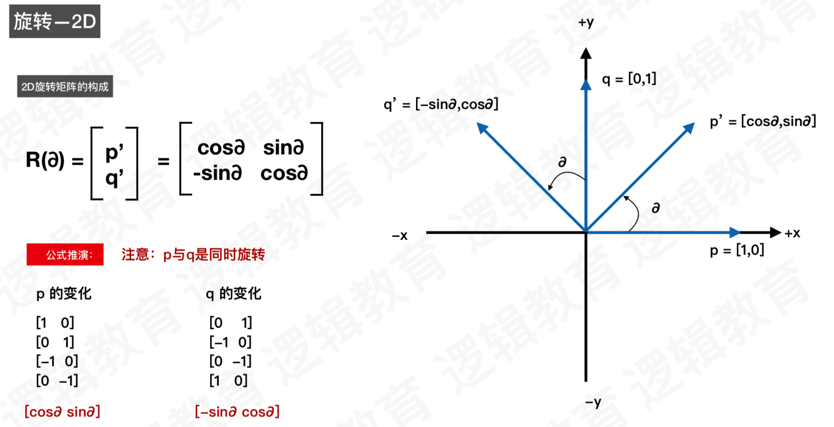
2、3D旋转矩阵(X轴)的构成
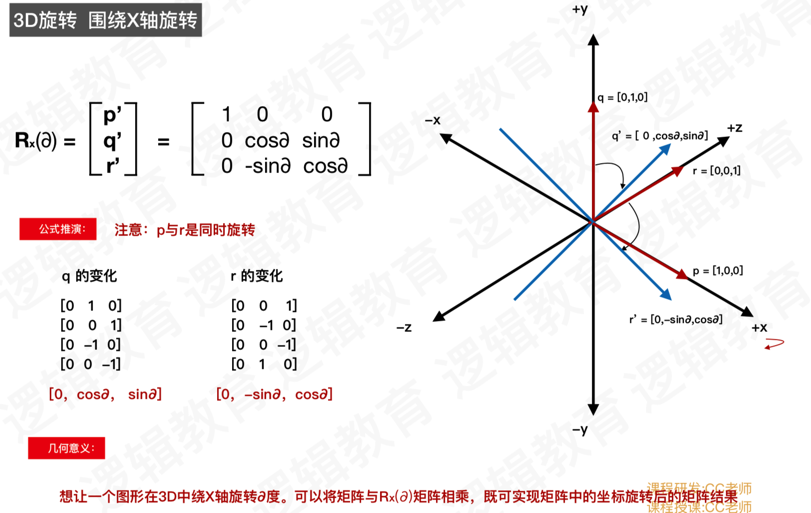
3、3D旋转矩阵(Y轴)的构成
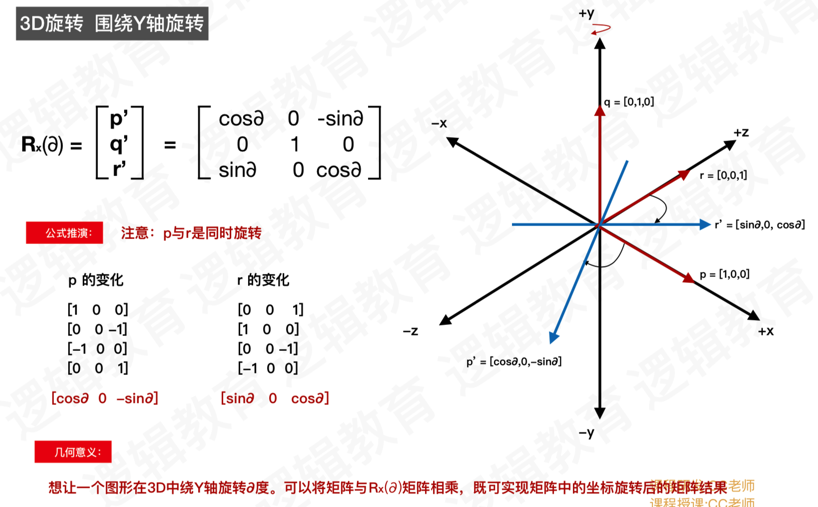
4、3D旋转矩阵(Z轴)的构成
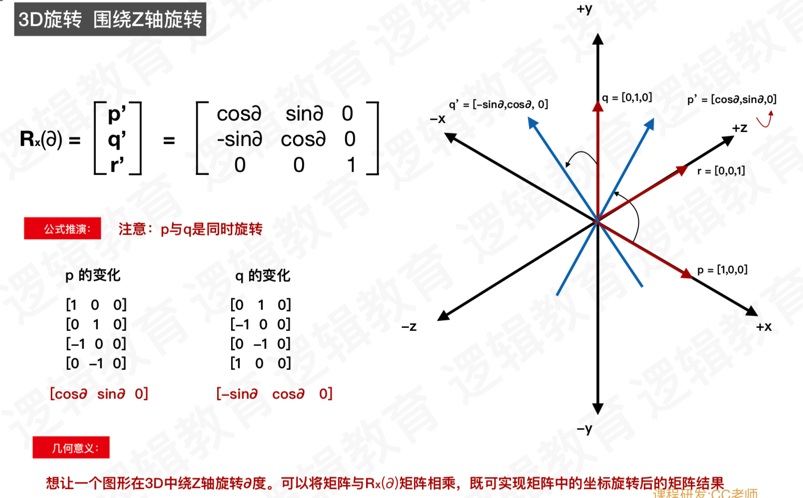
5、3D旋转矩阵(任意轴)的构成

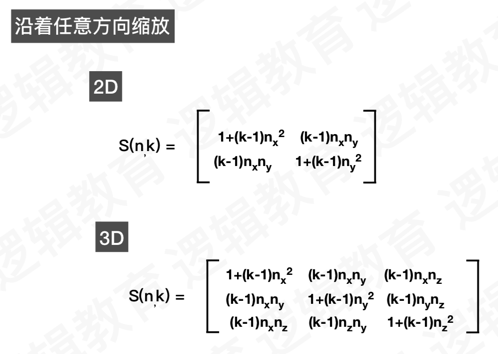
四、向量的缩放
矩阵M包含了旋转和缩放变化,单纯的缩放矩阵可以理解成是M的一个子集 (M缩放),(M缩放)它自身是有一些规律的。
1、2D缩放与3D缩放
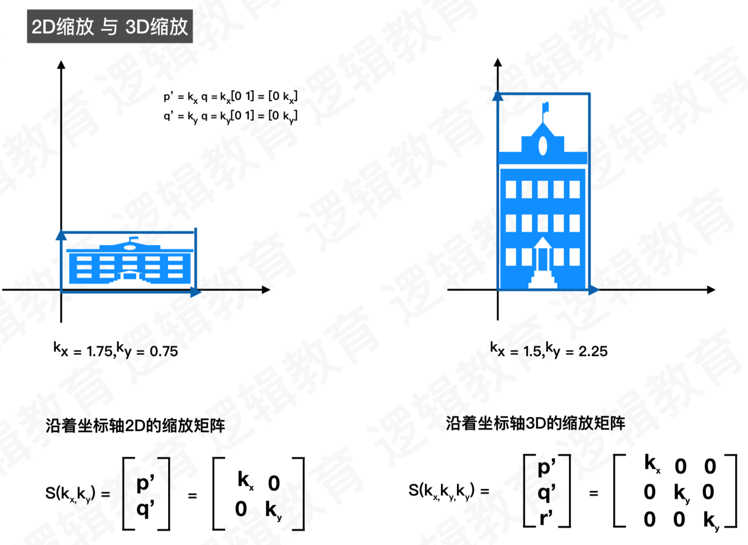
2、沿着任意方向缩放
行者常至,为者常成!
