目录
思考
一、设计一种数据结构
设计一种数据结构,用来存放整数,要求提供 3 个接口
添加元素
获取最大值
删除最大值
| 获取最大值 | 删除最大值 | 添加元素 | ||
| 动态数组\双向链表 | O(n) | O(n) | O(1) | |
| 有序动态数组\双向链表 | O(1) | O(1) | O(n) | 全排序有点浪费 |
| BBST | O(logn) | O(logn) | O(logn) | 杀鸡用了牛刀 |
有没有更优的数据结构? 堆
| 获取最大值 | 删除最大值 | 添加元素 | |
| 堆 | O(1) | O(logn) | O(logn) |
二、Top K问题
什么是 Top K 问题?
从海量数据中找出前 K 个数据
比如:从 100 万个整数中找出最大的 100 个整数
Top K 问题的解法之一:可以用数据结构“堆”来解决
堆
一、介绍
堆(Heap)也是一种树状的数据结构(不要跟内存模型中的“堆空间”混淆),常见的堆实现有
二叉堆(Binary Heap,完全二叉堆)
多叉堆(D-heap、D-ary Heap)
索引堆(Index Heap)
二项堆(Binomial Heap)
斐波那契堆(Fibonacci Heap)
左倾堆(Leftist Heap,左式堆)
斜堆(Skew Heap)
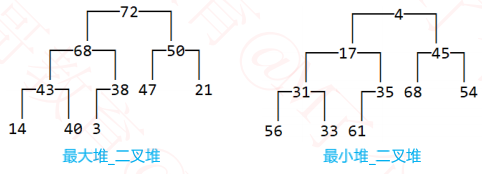
堆的一个重要性质:任意节点的值总是 ≥( ≤ )子节点的值
如果任意节点的值总是 ≥ 子节点的值,称为:最大堆、大根堆、大顶堆
如果任意节点的值总是 ≤ 子节点的值,称为:最小堆、小根堆、小顶堆
由此可见,堆中的元素必须具备可比较性(跟二叉搜索树一样)
二、堆的接口设计
/// 元素的数量
-(int)size;
/// 是否为空
-(BOOL)isEmpty;
/// 清空
-(void)clear;
/// 添加元素
-(void)add:(id)element;
/// 获得堆顶元素
-(id)get;
/// 删除堆顶元素
-(id)remove;
/// 删除堆顶元素的同时插入一个新元素
-(id)replace:(id)element;
二叉堆
二叉堆的逻辑结构就是一棵完全二叉树,所以也叫完全二叉堆
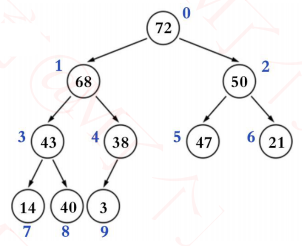
鉴于完全二叉树的一些特性,二叉堆的底层(物理结构)一般用数组实现即可
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 72 | 68 | 50 | 43 | 38 | 47 | 21 | 14 | 40 | 3 |
索引 i 的规律( n 是元素数量)
如果 i = 0 ,它是根节点
如果 i > 0 ,它的父节点的索引为 floor( (i – 1) / 2 )
如果 2i + 1 ≤ n – 1,它的左子节点的索引为 2i + 1
如果 2i + 1 > n – 1 ,它无左子节点
如果 2i + 2 ≤ n – 1 ,它的右子节点的索引为 2i + 2
如果 2i + 2 > n – 1 ,它无右子节点
一、获取最大值
/// 获得堆顶元素
-(id)get{
[self __emptyCheck];
return self.elements[0];
}
/// 检查元素数量是否为空
-(void)__emptyCheck{
if (self.size == 0) {
@throw [NSException exceptionWithName:@"LCBinaryHeap"
reason:@"Heap is empty"
userInfo:nil];;
}
}
二、最大堆添加
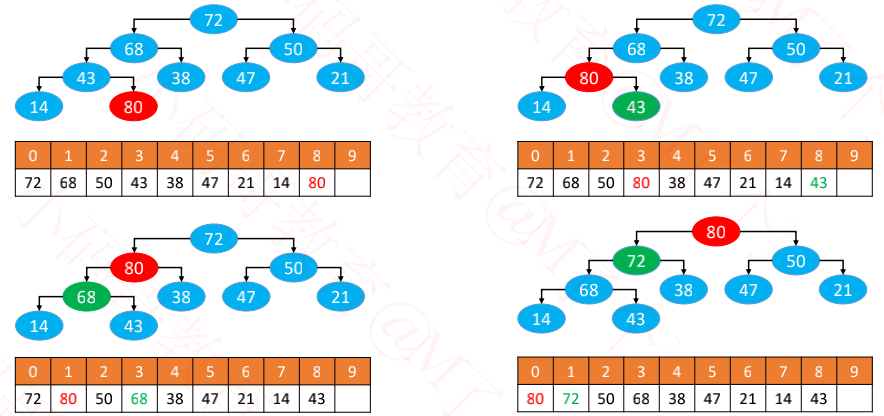
循环执行以下操作(图中的 80 简称为 node)
如果 node > 父节点,与父节点交换位置
如果 node ≤ 父节点,或者 node 没有父节点,退出循环
优化:将新添加节点备份,确定最终位置才摆放上去
这个过程,叫做上滤(Sift Up) 时间复杂度:O(logn)
三、最大堆删除
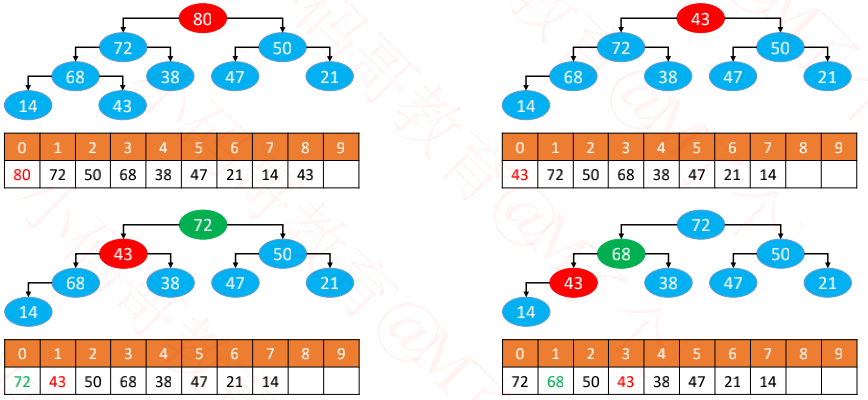
- 用最后一个节点覆盖根节点
- 删除最后一个节点
- 循环执行以下操作(图中的 43 简称为 node)
如果 node < 子节点,与最大的子节点交换位置
如果 node ≥ 子节点, 或者 node 没有子节点,退出循环
同样的,交换位置的操作可以像添加那样进行优化
这个过程,叫做下滤(Sift Down),时间复杂度:O(logn)
四、replace
-(id)replace:(id)element{
[self __elementNotNullCheck:element];
id root = nil;
if (self.size == 0) {
self.elements[0] = element;
self.size++;
}else{
root = self.elements[0];
self.elements[0] = element;
[self __siftDownWithIndex:0];
}
return root;
}
批量建堆
一、自上而下的上滤
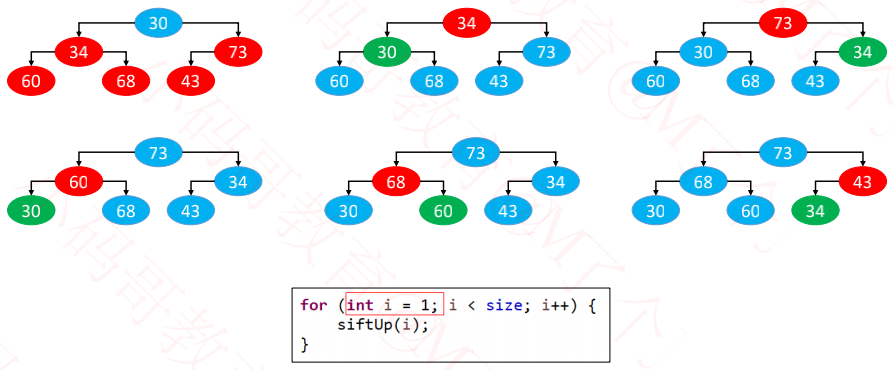
二、自下而上的下滤
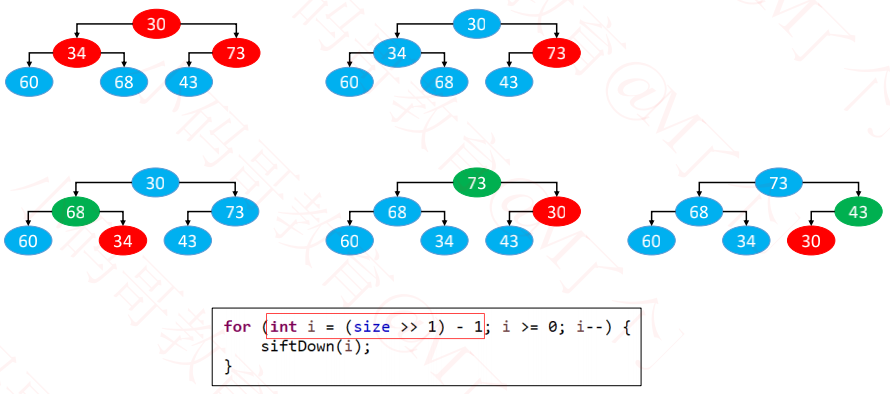
三、效率对比
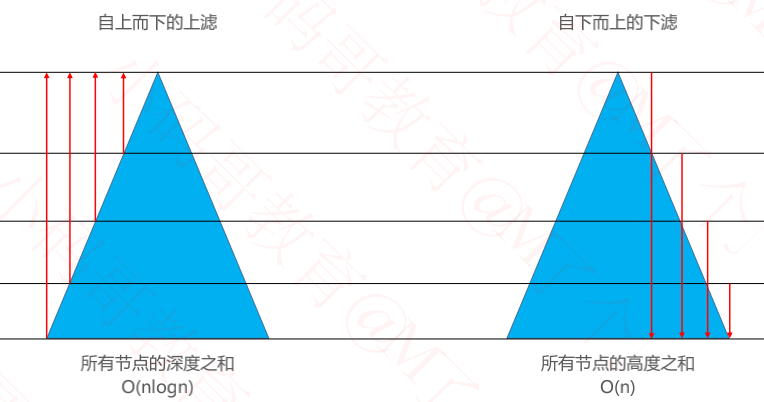
所有节点的深度之和
仅仅是叶子节点,就有近 n/2 个,而且每一个叶子节点的高度都是 O(logn) 级别的
因此,在叶子节点这一块,就达到了 O(nlogn) 级别
O(nlogn) 的时间复杂度足以利用排序算法对所有节点进行全排序
所有节点的高度之和
假设是满树,节点总个数为 n,树高为 h,那么 n = 2h − 1
所有节点的树高之和 H(n) = 20 ∗ h − 0 + 21 ∗ h − 1 + 22 ∗ h − 2 + ⋯ + 2h −1 ∗ h − h − 1
H(n) = h ∗ 20 + 21 + 22 + ⋯ + 2h −1 − 1 ∗ 21 + 2 ∗ 22 + 3 ∗ 23 + ⋯ + h − 1 ∗ 2h−1
H(n) = h ∗ 2h − 1 − h − 2 ∗ 2h + 2
H(n) = h ∗ 2h − h − h ∗ 2h + 2h+1 − 2
H(n) = 2h+1 − h − 2 = 2 ∗ (2h − 1) − h = 2n − h = 2n − log2(n + 1) = O(n)
四、思考
以下方法可以批量建堆么?
自上而下的下滤
自下而上的上滤
上述方法不可行,为什么?
认真思考【自上而下的上滤】、【自下而上的下滤】的本质
一个与添加逻辑相似、一个与删除逻辑相似
五、如何构建一个小顶堆
-(void)test{
self.heap = [LCBinaryHeap binaryHeapWithArray:@[@1,@2,@3,@4,@5,@6,@7]
comparator:^LCCompareType(id _Nonnull obj1, id _Nonnull obj2) {
//通过改变比较逻辑 可构建大顶堆和小顶堆
if ([obj1 intValue]<[obj2 intValue]) {
return LCCompareGreater;
}else if([obj1 intValue]>[obj2 intValue]){
return LCCompareLess;
}
return LCCompareEqual;
}];
}
Top K 问题
从 n 个整数中,找出最大的前 k 个数( k 远远小于 n )
如果使用排序算法进行全排序,需要 O(nlogn) 的时间复杂度
如果使用二叉堆来解决,可以使用 O(nlogk) 的时间复杂度来解决
新建一个小顶堆,扫描 n 个整数
✓ 先将遍历到的前 k 个数放入堆中
✓ 从第 k + 1 个数开始,如果大于堆顶元素,就使用 replace 操作(删除堆顶元素,将第 k + 1 个数添加到堆中)
扫描完毕后,堆中剩下的就是最大的前 k 个数
如果是找出最小的前 k 个数呢?
用大顶堆,如果小于堆顶元素,就使用 replace 操作
行者常至,为者常成!
