目录
哈夫曼编码(Huffman Coding)
哈夫曼编码，又称为霍夫曼编码，它是现代压缩算法的基础
假设要把字符串【ABBBCCCCCCCCDDDDDDEE】转成二进制编码进行传输
可以转成ASCII编码（65~69，1000001~1000101），但是有点冗长，如果希望编码更短呢？
可以先约定5个字母对应的二进制
| A | B | C | D | E |
| 000 | 001 | 010 | 011 | 100 |
对应的二进制编码：000001001001010010010010010010010010011011011011011011100100
如果使用ASCII编码，每个字母需要8个二进制位，20个字母需要160个二进制位。
如果按照上述规则，一共20个字母，转成了60个二进制位
如果使用哈夫曼编码，可以压缩至41个二进制位，约为原来长度的68.3%
哈弗曼树
先计算出每个字母的出现频率（权值，这里直接用出现次数），【ABBBCCCCCCCCDDDDDDEE】
| A | B | C | D | E |
| 1 | 3 | 8 | 6 | 2 |
利用这些权值，构建一棵哈夫曼树（又称为霍夫曼树、最优二叉树）
如何构建一棵哈夫曼树？（假设有 n 个权值）
- 以权值作为根节点构建 n 棵二叉树，组成森林
- 在森林中选出 2 个根节点最小的树合并，作为一棵新树的左右子树，且新树的根节点为其左右子树根节点之和
- 从森林中删除刚才选取的 2 棵树，并将新树加入森林
- 重复 2、3 步骤，直到森林只剩一棵树为止，该树即为哈夫曼树
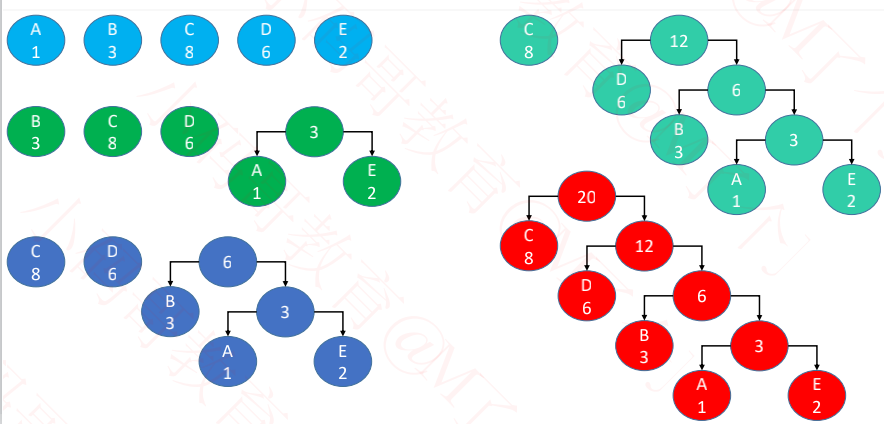
构建哈夫曼编码
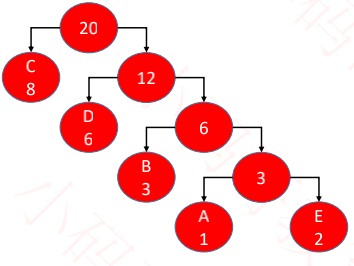
left为0，right为1，可以得出5个字母对应的哈夫曼编码
| A | B | C | D | E |
| 1110 | 110 | 0 | 10 | 1111 |
【ABBBCCCCCCCCDDDDDDEE】的哈夫曼编码是
1110110110110000000001010101010101111
总结
n 个权值构建出来的哈夫曼树拥有 n 个叶子节点
每个哈夫曼编码都不是另一个哈夫曼编码的前缀
哈夫曼树是带权路径长度最短的树，权值较大的节点离根节点较近
带权路径长度：树中所有的叶子节点的权值乘上其到根节点的路径长度。与最终的哈夫曼编码总长度成正比关系。
每一个编码都不是另外一个编码的前缀，这样就可以做到精准解析,不会产生歧义。
出现频率越高，使用的编码越短。出现频率越低使用的编码较长。降低了整个编码的大小
行者常至，为者常成！