目录
虚拟头节点
有时候为了让代码更加精简,统一所有节点的处理逻辑,可以在最前面增加一个虚拟的头结点(不存储数据)
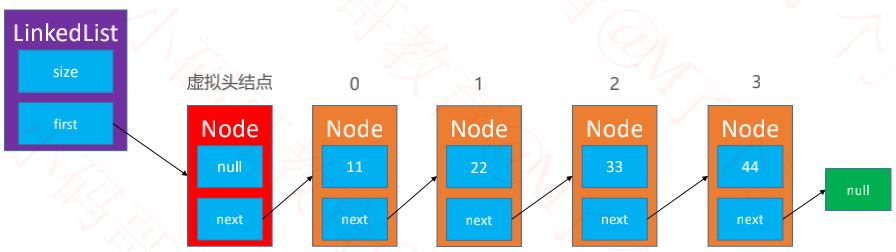
增加虚拟头结点后需要改动的方法
//初始化时创建虚拟头结点
-(instancetype)init{
self = [super init];
if (self) {
_first = [LCNode nodeWithElement:nil next:nil];
}
return self;
}
/// 获取index位置的node对象
/// @param index 索引
-(LCNode*)nodeForIndex:(int)index{
[self rangeCheck:index];
LCNode * node = _first.next;
for (int i=0; i<index; i++) {
node = node.next;
}
return node;
}
- (int)indexOf:(nonnull id)element {
LCNode * node = _first.next;
for (int i = 0; i<_size; i++) {
if ([element isEqual:node.element]) {
return i;
}
node = node.next;
}
return ELEMENT_NOT_FOUND;
}
- (void)add:(int)index element:(nonnull id)element {
[self rangeCheckForAdd:index];
//first -> headerNode -> node0 -> node1 -> node2
//增加头结点之后,处理上更加统一,都可以拿到一个preNode
//但额外增加了内存占用
LCNode * preNode = index == 0?_first:[self nodeForIndex:index-1];
preNode.next = [LCNode nodeWithElement:element next:preNode.next];
_size++;
}
- (nonnull id)remove:(int)index {
[self rangeCheck:index];
//first -> headerNode -> node0 -> node1 -> node2
LCNode * preNode = index == 0?_first:[self nodeForIndex:index-1];
LCNode * node = preNode.next;
preNode.next = node.next;
_size--;
return node.element;
}
-(NSString *)description{
NSMutableString * des = [NSMutableString stringWithFormat:@"size=%d, [",_size];
LCNode * node = _first.next;
for (int i=0; i<_size; i++) {
if (i!=0) {
[des appendString:@", "];
}
[des appendFormat:@"%@",node];
node = node.next;
}
[des appendString:@"]"];
return des;
}
动态数组的缩容
如果内存使用比较紧张,动态数组有比较多的剩余空间,可以考虑进行缩容操作
比如剩余空间占总容量的一半时,就进行缩容
如果扩容倍数、缩容时机设计不得当,有可能会导致复杂度震荡(比如:扩容时机选择为2倍、缩容时机选择为1/2时,在1/2位置处频繁的进行删除或添加元素操作时会交替进行扩容和缩容操作。)
/// 删除index位置的元素
/// @param index 位置
-(nonnull id)remove:(int)index{
[self rangeCheck:index];
void* old = _elements[index];
for (int i = index+1; i<_size; i++) {
_elements[i-1] = _elements[i];
}
_elements[--_size] = NULL;
[self trim];
return (__bridge id)old;
}
-(void)trim{
int oldCapacity = _capacity;
int newCapacity = oldCapacity>>1;
if (_size>newCapacity || oldCapacity<=DEFAULT_CAPACITY) {
return;
}
int memorysize = newCapacity*sizeof(void*);
void** newElements = malloc(memorysize);
for (int i = 0; i < _size; i++) {
newElements[i] = _elements[i];
}
if (_elements) {
free(_elements);
_elements = nil;
}
_elements = newElements;
_capacity = newCapacity;
NSLog(@"%d 缩容为 %d",oldCapacity,newCapacity);
}
/// 清除所有元素
-(void)clear{
for (int i=0; i<_size; i++) {
_elements[i] = nil;
}
_size = 0;
if (_elements!=nil && _capacity >DEFAULT_CAPACITY) {
int memorySize = DEFAULT_CAPACITY*sizeof(void*);
_elements = (void**)malloc(memorySize);
}
}
双向链表
一、双向链表图示
1、多节点
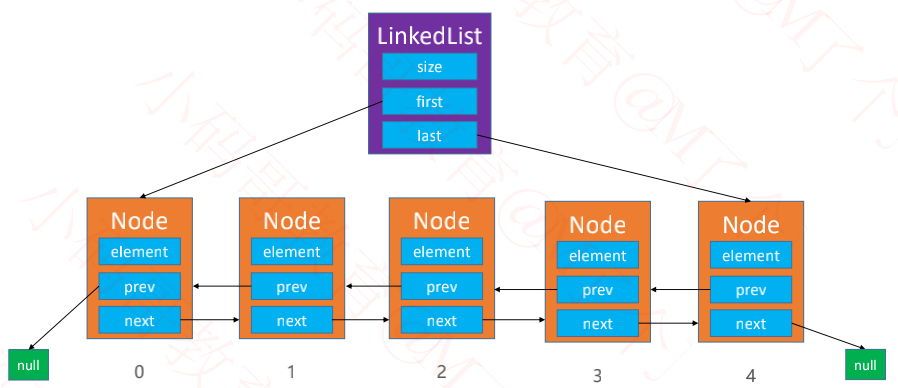
2、单节点
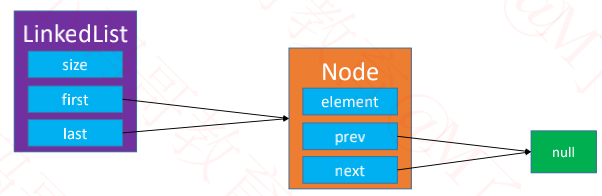
二、使用双向链表可以提升链表的综合性能
1、
粗略对比一下删除的操作数量
单向链表:1 + 2 + 3 + … + n 除以n平均一下是 1/2+n/2
双向链表:(1 + 2 + 3 + … +n/2) * 2 =除以n平均一下是 1/2+n/4
操作数量缩减了近一半
2、
动态数组:开辟、销毁内存空间的次数相对较少,但可能造成内存空间浪费(可以通过缩容解决)
◼ 双向链表:开辟、销毁内存空间的次数相对较多,但不会造成内存空间的浪费
◼ 如果频繁在尾部进行添加、删除操作,动态数组、双向链表均可选择
◼ 如果频繁在头部进行添加、删除操作,建议选择使用双向链表
◼ 如果有频繁的(在任意位置)添加、删除操作,建议选择使用双向链表
◼ 如果有频繁的查询操作(随机访问操作),建议选择使用动态数组
3、
有了双向链表,单向链表是否就没有任何用处了?
并非如此,在哈希表的设计中就用到了单链表
至于原因,在哈希表章节中会讲到
复杂度分析
一、从下面几个方面分析复杂度
最好情况复杂度
最坏情况复杂度
平均情况复杂度
均摊复杂度
二、数组的随机访问
| 索引 | 元素 |
| 0 | 11 |
| 1 | 22 |
| 2 | 33 |
| 3 | 44 |
| 4 | 55 |
| 5 | 66 |
数组的随机访问速度非常快
elements[n]的效率与n是多少无关
三、复杂度对比
| 动态数组 | 最好 | 最坏 | 平均 |
| add(int index, E element) | O(1) | O(n) | O(n) |
| remove(int index) | O(1) | O(n) | O(n) |
| set(int index, E element) | O(1) | O(1) | O(1) |
| get(int index) | O(1) | O(1) | O(1) |
| 链表 | 最好 | 最坏 | 平均 |
| add(int index, E element) | O(1) | O(n) | O(n) |
| remove(int index) | O(1) | O(n) | O(n) |
| set(int index, E element) | O(1) | O(n) | O(n) |
| get(int index) | O(1) | O(n) | O(n) |
动态数组add(E element)复杂度分析
| 最好 | O(1) |
| 最坏(需要扩容时) | O(n) |
| 平均 | O(1) |
| 均摊 | O(1) |
什么情况下适合使用均摊复杂度
经过连续的多次复杂度比较低的情况后,出现个别复杂度比较高的情况
行者常至,为者常成!
