目录
初识排序
一、什么叫排序?
排序前:3,1,6,9,2,5,8,4,7
排序后:1,2,3,4,5,6,7,8,9(升序) 或者 9,8,7,6,5,4,3,2,1(降序)
排序的应用无处不在
二、十大排序算法
| 名称 | 时间复杂度(最好) | 时间复杂度(最坏) | 时间复杂度((平均) | 空间复杂度 | In-place | 稳定性 |
| 冒泡排序(Bubble Sort) | O(n) | O(n^2) | O(n^2) | O(1) | ✔ | ✔ |
| 选择排序(Selection Sort) | O(n^2) | O(n^2) | O(n^2) | O(1) | ✔ | ❌ |
| 插入排序(Insertion Sort) | O(n) | O(n^2) | O(n^2) | O(1) | ✔ | ✔ |
| 归并排序(Merge Sort) | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | ❌ | ✔ |
| 快速排序(Quick Sort) | O(nlogn) | O(n^2) | O(nlogn) | O(logn) | ✔ | ❌ |
| 希尔排序(Shell Sort) | O(n) | O(n4/3) ~ O(n^2) | 取决于步长序列 | O(1) | ✔ | ❌ |
| 堆排序(Heap Sort) | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | ✔ | ❌ |
| 计数排序(Counting Sort) | O(n + k) | O(n + k) | O(n + k) | O(n + k) | ❌ | ✔ |
| 基数排序(Radix Sort) | O(d ∗ (n + k)) | O(d ∗ (n + k)) | O(d ∗ (n + k)) | O(n + k) | ❌ | ✔ |
| 桶排序(Bucket Sort) | O(n + k) | O(n + k) | O(n + k) | O(n + m) | ❌ | ✔ |
以上表格是基于数组进行排序的一般性结论
冒泡、选择、插入、归并、快速、希尔、堆排序,属于比较排序(Comparison Sorting)
冒泡排序(Bubble Sort)
一、Bubble Sort
冒泡排序也叫做起泡排序
执行流程(统一以升序为例子)
① 从头开始比较每一对相邻元素,如果第1个比第2个大,就交换它们的位置
执行完一轮后,最末尾那个元素就是最大的元素
② 忽略 ① 中曾经找到的最大元素,重复执行步骤 ①,直到全部元素有序
//时间复杂度:最好O(n^2)、最坏O(n^2)、平均O(n^2)
//空间复杂度O(1)
+(void)bubbleSort:(NSMutableArray*)array{
for (int end = (int)array.count; end>1; end--) {
for (int i = 1; i<end; i++) {
if ([array[i-1] compare:array[i]] == NSOrderedDescending ) {
id temp = array[i-1];
array[i-1] = array[i];
array[i] = temp;
}
NSLog(@"执行次数%d_%d",end,i);
}
}
}
二、优化1
如果序列已经完全有序,可以提前终止冒泡排序
//时间复杂度:最好O(n)、最坏O(n^2)、平均O(n^2)
//空间复杂度O(1)
+(void)bubbleSort2:(NSMutableArray*)array{
for (int end = (int)array.count; end>1; end--) {
BOOL sorted = true;
for (int i = 1; i<end; i++) {
if ([array[i-1] compare:array[i]] == NSOrderedDescending ) {
id temp = array[i-1];
array[i-1] = array[i];
array[i] = temp;
//发生了交换
sorted = false;
}
NSLog(@"执行次数%d_%d",end,i);
}
//没有发生交换,已经全部排序完成。
if(sorted) break;
}
}
三、优化2
如果序列尾部已经局部有序,可以记录最后1次交换的位置,减少比较次数
//时间复杂度:最好O(n)、最坏O(n^2)、平均O(n^2)
//空间复杂度O(1)
+(void)bubbleSort3:(NSMutableArray*)array{
for (int end = (int)array.count; end>1; end--) {
int index = 1;
for (int i = 1; i<end; i++) {
if ([array[i-1] compare:array[i]] == NSOrderedDescending ) {
id temp = array[i-1];
array[i-1] = array[i];
array[i] = temp;
//记录最后一次发生交换的index
index = i;
}
NSLog(@"执行次数%d_%d",end,i);
}
//index及之后的数据已经排布好,不需要再次进行判断及交换
end = index+1;
}
}
四、排序算法的稳定性(Stability)
如果相等的2个元素,在排序前后的相对位置保持不变,那么这是稳定的排序算法
排序前:5, 1, 3𝑎, 4, 7, 3𝑏
稳定的排序: 1, 3𝑎, 3𝑏, 4, 5, 7
不稳定的排序:1, 3𝑏, 3𝑎, 4, 5, 7
对自定义对象进行排序时,稳定性会影响最终的排序效果
冒泡排序属于稳定的排序算法
稍有不慎,稳定的排序算法也能被写成不稳定的排序算法,比如下面的冒泡排序代码是不稳定的
//时间复杂度:最好O(n^2)、最坏O(n^2)、平均O(n^2)
//空间复杂度O(1)
+(void)bubbleSort:(NSMutableArray*)array{
for (int end = (int)array.count; end>1; end--) {
for (int i = 1; i<end; i++) {
if ([array[i-1] compare:array[i]] >=0 ) {
id temp = array[i-1];
array[i-1] = array[i];
array[i] = temp;
}
NSLog(@"执行次数%d_%d",end,i);
}
}
}
五、原地算法(In-place Algorithm)
何为原地算法?
不依赖额外的资源或者依赖少数的额外资源,仅依靠输出来覆盖输入
空间复杂度为 𝑂(1) 的都可以认为是原地算法
非原地算法,称为 Not-in-place 或者 Out-of-place
冒泡排序属于 In-place
选择排序(Selection Sort)
一、原理及实现
执行流程
① 从序列中找出最大的那个元素,然后与最末尾的元素交换位置
✓ 执行完一轮后,最末尾的那个元素就是最大的元素
② 忽略 ① 中曾经找到的最大元素,重复执行步骤 ①
//时间复杂度:最好O(n^2)、最坏O(n^2)、平均O(n^2)
//空间复杂度O(1)
-(void)sort{
for (int end = (int)self.array.count; end>0; end--) {
NSUInteger maxIndex = 0;
for (int i = 1; i<end; i++) {
/**
4 3 6 10 10 2 5 2
<0 算法是不稳定的,像上面会将前面的10放到后面
<=0 虽然能保证后面的10 依然在后面,但也不能保证算法的稳定性 比如说2
既然算法是不稳定的,那么下边<=0 就可以写成 < 0,减少比较次数提高性能
*/
//if ([self compareWithIndex1:maxIndex index2:i]<=0) {
if ([self compareWithIndex1:maxIndex index2:i]<0) {
maxIndex = i;
}
}
[self swapWitnIndex1:maxIndex index2:end-1];
}
}
选择排序的交换次数要远远少于冒泡排序,平均性能优于冒泡排序
最好、最坏、平均时间复杂度:O(n^2),空间复杂度:O(1),属于不稳定排序
二、思考
选择排序是否还有优化的空间?
使用堆来选择最大值
堆排序(Heap Sort)
一、原理
堆排序可以认为是对选择排序的一种优化
执行流程
① 对序列进行原地建堆(heapify)
② 重复执行以下操作,直到堆的元素数量为1
✓ 交换堆顶元素与尾元素
✓ 堆的元素数量减 1
✓ 对 0 位置进行 1 次 siftDown 操作
| 0 | 1 | 2 | 3 | 4 | 5 |
| 50 | 21 | 80 | 43 | 38 | 14 |
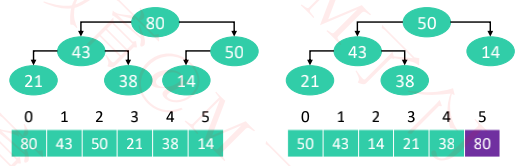

二、实现
//时间复杂度:最好O(nlogn)、最坏O(nlogn)、平均O(nlogn)
//空间复杂度O(1)
-(void)sort{
self.size = (int)self.array.count;
//批量建堆
[self __heapify];
//交换位置并下滤
while (self.size>1) {
// 交换堆顶元素和尾部元素
[self swapWitnIndex1:0 index2:--self.size];
// 对0位置进行siftDown(恢复堆的性质)
[self __siftDownWithIndex:0];
}
}
#pragma mark - 内部方法
/// 批量建堆
-(void)__heapify{
// 自下而上的下滤
for (int i = (self.size >> 1) - 1; i >= 0; i--) {
[self __siftDownWithIndex:i];
}
}
/// 下滤索引对应的元素
/// @param index 索引
-(void)__siftDownWithIndex:(int)index{
if(self.size == 0) return;
id element = self.array[index];
//非叶子节点的数量
//第一个叶子节点的索引
int half = self.size >> 1;
//必须保证index位置是非叶子节点
while (index<half) {
//index的节点有2种情况
//1、只有左子节点
//2、同时有左右子节点
//默认为左子节点跟它进行比较
int childIndex = (index<<1)+1;
id child = self.array[childIndex];
//右子节点
int rightIndex = childIndex+1;
//选出左右子节点最大的那个
if (rightIndex<self.size &&[self compareWithValue1:self.array[rightIndex] value2:child]>0) {
child = self.array[childIndex = rightIndex];
}
if( [self compareWithValue1:element value2:child] > 0) break;
//将子节点存放到index的位置
self.array[index] = child;
index = childIndex;
}
self.array[index] = element;
}
最好、最坏、平均时间复杂度:O(nlogn),空间复杂度:O(1),属于不稳定排序
行者常至,为者常成!
