目录
贪心(Greedy)
一、贪心
贪心策略,也称为贪婪策略
每一步都采取当前状态下最优的选择(局部最优解),从而希望推导出全局最优解
贪心的应用
哈夫曼树
最小生成树算法:Prim、Kruskal
最短路径算法:Dijkstra
二、最优装载问题(加勒比海盗)
在北美洲东南部,有一片神秘的海域,是海盗最活跃的加勒比海
有一天,海盗们截获了一艘装满各种各样古董的货船,每一件古董都价值连城,一旦打碎就失去了它的价值
海盗船的载重量为 W,每件古董的重量为 𝑤i,海盗们该如何把尽可能多数量的古董装上海盗船?
比如 W 为 30,𝑤i 分别为 3、5、4、10、7、14、2、11
贪心策略:每一次都优先选择重量最小的古董
① 选择重量为 2 的古董,剩重量 28
② 选择重量为 3 的古董,剩重量 25
③ 选择重量为 4 的古董,剩重量 21
④ 选择重量为 5 的古董,剩重量 16
⑤ 选择重量为 7 的古董,剩重量 9
最多能装载 5 个古董
+(void)pirate{
NSArray * weights = @[@3,@5,@4,@10,@7,@14,@2,@11];
weights = [weights sortedArrayUsingComparator:^NSComparisonResult(id _Nonnull obj1, id _Nonnull obj2) {
return [obj1 compare:obj2];
}];
int capacity = 30,weight = 0,count = 0;
for (int i = 0; i<weights.count && weight<capacity; i++) {
int newWeight = weight + [weights[i] intValue];
if (newWeight<=capacity) {
weight = newWeight;
count++;
NSLog(@"%@",weights[i]);
}
}
NSLog(@"一共选了 %d 件古董",count);
}
+(void)pirate2{
NSArray * weights = @[@3,@5,@4,@10,@7,@14,@2,@11];
weights = [weights sortedArrayUsingComparator:^NSComparisonResult(id _Nonnull obj1, id _Nonnull obj2) {
return [obj1 compare:obj2];
}];
int capacity = 30,count = 0;
for (int i = 0; i<weights.count; i++) {
if ((capacity -= [weights[i] intValue])>0) {
count++;
NSLog(@"%@",weights[i]);
}else{
break;
}
}
NSLog(@"一共选了 %d 件古董",count);
}
三、零钱兑换
1、例子1
假设有 25 分、10 分、5 分、1 分的硬币,现要找给客户 41 分的零钱,如何办到硬币个数最少?
贪心策略:每一次都优先选择面值最大的硬币
① 选择 25 分的硬币,剩 16 分
② 选择 10 分的硬币,剩 6 分
③ 选择 5 分的硬币,剩 1 分
④ 选择 1 分的硬币
最终的解是共 4 枚硬币
25 分、10 分、5 分、1 分硬币各一枚
/// 零钱兑换问题
+(void)coinChange{
NSArray * coins = @[@5,@1,@10,@25];
coins = [coins sortedArrayUsingComparator:^NSComparisonResult(id _Nonnull obj1, id _Nonnull obj2) {
return [obj1 compare:obj2];
}];
int change = 41,index = (int)coins.count-1,count = 0;
while (index>=0 && change > 0) {
int newChange = change - [coins[index] intValue];
if (newChange >= 0) {
change = newChange;
count++;
NSLog(@"%@ 分",coins[index]);
}else{
index--;
}
}
NSLog(@"共选择了 %d 枚硬币",count);
}
2、例子2
假设有 25 分、20 分、5 分、1 分的硬币,现要找给客户 41 分的零钱,如何办到硬币个数最少?
贪心策略:每一步都优先选择面值最大的硬币
① 选择 25 分的硬币,剩 16 分
② 选择 5 分的硬币,剩 11 分
③ 选择 5 分的硬币,剩 6 分
④ 选择 5 分的硬币,剩 1 分
⑤ 选择 1 分的硬币
最终的解是 1 枚 25 分、3 枚 5 分、1 枚 1 分的硬币,共 5 枚硬币
实际上本题的最优解是:2 枚 20 分、1 枚 1 分的硬币,共 3 枚硬币
注意
贪心策略并不一定能得到全局最优解
因为一般没有测试所有可能的解,容易过早做决定,所以没法达到最佳解
贪图眼前局部的利益最大化,看不到长远未来,走一步看一步
优点:简单、高效、不需要穷举所有可能,通常作为其他算法的辅助算法来使用
缺点:鼠目寸光,不从整体上考虑其他可能,每次采取局部最优解,不会再回溯,因此很少情况会得到最优解
四、0-1背包
有 n 件物品和一个最大承重为 W 的背包,每件物品的重量是 𝑤i、价值是 𝑣i
在保证总重量不超过 W 的前提下,将哪几件物品装入背包,可以使得背包的总价值最大?
注意:每个物品只有 1 件,也就是每个物品只能选择 0 件或者 1 件,因此称为 0-1背包问题
如果采取贪心策略,有3个方案
① 价值主导:优先选择价值最高的物品放进背包
② 重量主导:优先选择重量最轻的物品放进背包
③ 价值密度主导:优先选择价值密度最高的物品放进背包(价值密度 = 价值 ÷ 重量)
假设背包最大承重150,7个物品如表格所示
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 重量 | 35 | 30 | 60 | 50 | 40 | 10 | 25 |
| 价值 | 10 | 40 | 30 | 50 | 35 | 40 | 30 |
| 价值密度 | 0.29 | 1.33 | 0.5 | 1.0 | 0.88 | 4.0 | 1.2 |
① 价值主导:放入背包的物品编号是 4、2、6、5,总重量 130,总价值 165
② 重量主导:放入背包的物品编号是 6、7、2、1、5,总重量 140,总价值 155
③ 价值密度主导:放入背包的物品编号是 6、2、7、4、1,总重量 150,总价值 170
代码实现
#import "LCKnapsack.h"
@interface LCArticle:NSObject
@property(nonatomic,assign)int weight;
@property(nonatomic,assign)int value;
@property(nonatomic,assign)double valueDensity;
+(instancetype)articleWeight:(int)weight value:(int)value;
@end
@implementation LCArticle
+(instancetype)articleWeight:(int)weight value:(int)value{
LCArticle * article = [[LCArticle alloc] init];
article.weight = weight;
article.value = value;
article.valueDensity = value * 1.0 / weight;
return article;
}
-(NSString *)description{
NSString * weight = [NSString stringWithFormat:@"weight=%d",_weight];
NSString * value = [NSString stringWithFormat:@"value=%d",_value];
NSString * valueDensity = [NSString stringWithFormat:@"valueDensity=%.2lf",_valueDensity];
return [NSString stringWithFormat:@"%@,%@,%@",weight,value,valueDensity];
}
@end
#pragma mark -
#pragma mark -
@implementation LCKnapsack
/// 0-1背包问题
+(void)knapsack{
[self __knapsackTitle:@"重量主导" comparator:^NSComparisonResult(LCArticle* obj1, LCArticle* obj2) {
//按照weight升序排列
return obj1.weight - obj2.weight;
}];
[self __knapsackTitle:@"价值主导" comparator:^NSComparisonResult(LCArticle* obj1, LCArticle* obj2) {
//按照value降序排列
return obj2.value - obj1.value;
}];
[self __knapsackTitle:@"价值密度主导" comparator:^NSComparisonResult(LCArticle* obj1, LCArticle* obj2) {
//由于浮点数的精度问题,不能通过相减来判断是否相等
//浮点返回 0.3 会被强转为int认为是0 使结果不准
// double result = obj2.valueDensity - obj1.valueDensity;
// NSLog(@"result = %lf",result);
// return result;
//按照valueDensity降序排列
if (obj1.valueDensity > obj2.valueDensity) {
return -1;
}else if (obj2.valueDensity > obj1.valueDensity){
return 1;
}else{
return 0;
}
}];
}
+(void)__knapsackTitle:(NSString*)title comparator:(NSComparator)comparator{
NSArray * articles = @[
[LCArticle articleWeight:35 value:10],
[LCArticle articleWeight:30 value:40],
[LCArticle articleWeight:60 value:30],
[LCArticle articleWeight:50 value:50],
[LCArticle articleWeight:40 value:35],
[LCArticle articleWeight:10 value:40],
[LCArticle articleWeight:25 value:30],
];
articles = [articles sortedArrayUsingComparator:comparator];
NSMutableArray * selected = [NSMutableArray array];
int capacity = 150, weight = 0, value = 0;
for (LCArticle* article in articles) {
if (weight>=capacity) break;
int newWeight = weight + article.weight;
if (newWeight <= capacity) {
weight = newWeight;
value += article.value;
[selected addObject:article];
}
}
NSLog(@"【 %@ 】",title);
NSLog(@"总价值:%d,总重量:%d",value,weight);
for (LCArticle * article in selected) {
NSLog(@"%@",article);
}
NSLog(@"-------------------------------");
}
@end
【 重量主导 】
总价值:155,总重量:140
weight=10,value=40,valueDensity=4.00
weight=25,value=30,valueDensity=1.20
weight=30,value=40,valueDensity=1.33
weight=35,value=10,valueDensity=0.29
weight=40,value=35,valueDensity=0.88
——————————-
【 价值主导 】
总价值:165,总重量:130
weight=50,value=50,valueDensity=1.00
weight=30,value=40,valueDensity=1.33
weight=10,value=40,valueDensity=4.00
weight=40,value=35,valueDensity=0.88
——————————-
【 价值密度主导 】
总价值:170,总重量:150
weight=10,value=40,valueDensity=4.00
weight=30,value=40,valueDensity=1.33
weight=25,value=30,valueDensity=1.20
weight=50,value=50,valueDensity=1.00
weight=35,value=10,valueDensity=0.29
——————————-
分治(Divide And Conquer)
一、分支策略
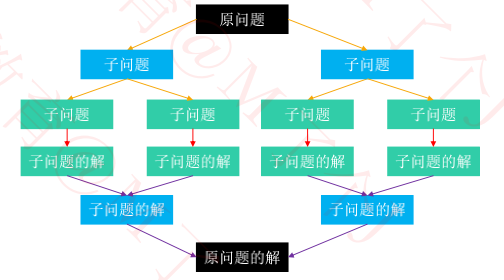
分治,也就是分而治之。它的一般步骤是
① 将原问题分解成若干个规模较小的子问题(子问题和原问题的结构一样,只是规模不一样)
② 子问题又不断分解成规模更小的子问题,直到不能再分解(直到可以轻易计算出子问题的解)
③ 利用子问题的解推导出原问题的解
因此,分治策略非常适合用递归
需要注意的是:子问题之间是相互独立的
分治的应用
快速排序
归并排序
Karatsuba算法(大数乘法)
二、主定理
分治策略通常遵守一种通用模式

思考:为什么有些问题采取分治策略后,性能会有所提升?
比如:时间复杂度为log(n^2)的算法,分解为 2个 log((n/2)^) 的算法 时间复杂度变为 log(n^2/2)
三、最大连续子序列和
给定一个长度为 n 的整数序列,求它的最大连续子序列和
比如 –2、1、–3、4、–1、2、1、–5、4 的最大连续子序列和是 4 + (–1) + 2 + 1 = 6
这道题也属于最大切片问题(最大区段,Greatest Slice)
概念区分
子串、子数组、子区间必须是连续的,子序列是可以不连续的
1、解法一:暴力出奇迹
穷举出所有可能的连续子序列,并计算出它们的和,最后取它们中的最大值
/// 求最大连续子序列合
/// @param array 序列
+(int)maxSubArray:(NSArray*)array{
if (array == nil || array.count == 0) return -1;
int beginIdx = 0;
int endIdx = 0;
int maxSum = [array[0] intValue];
for (int begin = 0; begin<array.count; begin++) {
for (int end = begin; end<array.count; end++) {
int sum = 0;
for (int i = begin; i<=end; i++) {
sum += [array[i] intValue];
}
if (sum > maxSum) {
maxSum = sum;
beginIdx = begin;
endIdx = end;
}
}
}
NSLog(@"beginIdx = %d,endIdx = %d",beginIdx,endIdx);
return maxSum;
}
空间复杂度:O(1),时间复杂度:O(n^3)
2、暴力出奇迹优化
重复利用前面计算过的结果
/// 求最大连续子序列合(优化)
/// @param array 序列
+(int)maxSubArray2:(NSArray*)array{
if (array == nil || array.count == 0) return -1;
int beginIdx = 0;
int endIdx = 0;
int maxSum = [array[0] intValue];
for (int begin = 0; begin<array.count; begin++) {
int sum = 0;
for (int end = begin; end<array.count; end++) {
sum += [array[end] intValue];
if (sum > maxSum) {
maxSum = sum;
beginIdx = begin;
endIdx = end;
}
}
}
NSLog(@"beginIdx = %d,endIdx = %d",beginIdx,endIdx);
return maxSum;
}
空间复杂度:O(1),时间复杂度:O(n^2)
3、分治
将序列均匀地分割成 2 个子序列
[begin , end) = [begin , mid) + [mid , end),mid = (begin + end) » 1
假设 [begin , end) 的最大连续子序列和是 S[i , j) ,那么它有 3 种可能
S[i , j) 存在于 [begin , mid) 中,同时 S[i , j) 也是 [begin , mid) 的最大连续子序列和
S[i , j) 存在于 [mid , end) 中,同时 S[i , j) 也是 [mid , end) 的最大连续子序列和
S[i , j) 一部分存在于 [begin , mid) 中,另一部分存在于 [mid , end) 中
✓ S[i , j) = S[i , mid) + S[mid , j)
✓ S[i , mid) = max { S[k , mid) },begin ≤ k < mid
✓ S[mid , j) = max { S[mid , k) },mid < k ≤ end

/// 求最大连续子序列合(分治)
/// @param array 序列
+(int)maxSubArray3:(NSArray*)array{
return [self __maxSubArray3:array begin:0 end:(int)array.count];
}
+(int)__maxSubArray3:(NSArray*)array begin:(int)begin end:(int)end{
if (end - begin < 2) return [array[begin] intValue];
int mid = (begin + end) >> 1;
int leftMax = [array[mid-1] intValue];
int leftSum = leftMax;
for (int i = mid-2; i>=0; i--) {
leftSum += [array[i] intValue];
leftMax = MAX(leftSum, leftMax);
}
int rightMax = [array[mid] intValue];
int rightSum = rightMax;
for (int i = mid+1; i<=array.count-1; i++) {
rightSum += [array[i] intValue];
rightMax = MAX(rightSum, rightMax);
}
//跨越了左右两部分的最大值
int lrMax = leftMax+rightMax;
//左侧最大值
int lMax = [self __maxSubArray3:array begin:begin end:mid];
//右侧最大值
int rMax = [self __maxSubArray3:array begin:mid+1 end:end];
return MAX( lrMax,MAX(lMax,rMax));
}
空间复杂度:O(logn)
时间复杂度:O(nlogn)
跟归并排序、快速排序一样
T n = 2T(n^2) + O(n)
大数乘法
2个超大的数(比如2个100位的数),如何进行乘法?
拿64位的操作系统来说,能表示的最大整数是 64个bit为全部为1,那么两个100位的整数相乘必然超过了计算机能表示的最大范围。
用字符串来实现大数相乘。
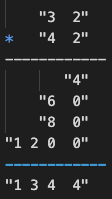
按照小学时学习的乘法运算,在进行 n 位数之间的相乘时,需要大约进行 n^2 次个位数的相乘
比如计算 36 x 54
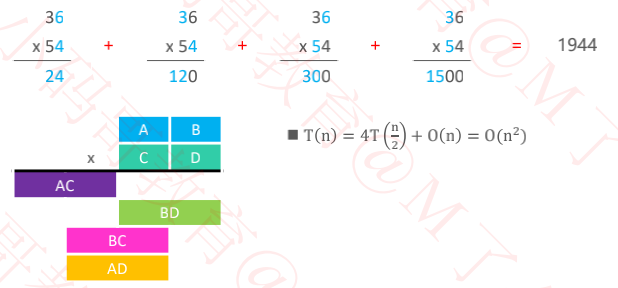
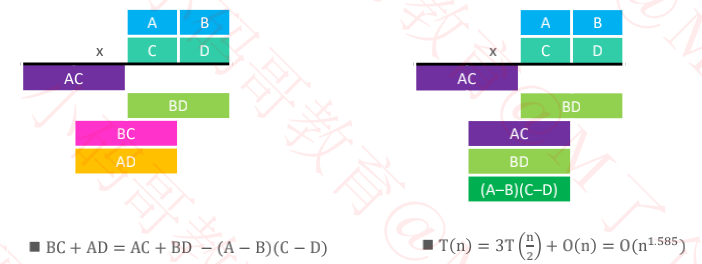
1960 年 Anatolii Alexeevitch Karatsuba 提出了 Karatsuba 算法,提高了大数乘法的效率
行者常至,为者常成!
