传统与现代加密技术

2015-06-07 | 阅读：

传统加密方法

传统的加密方式主要采用替代和换位两种方式，来混淆要加密的内容，解密时对照密码本进行恢复。

替代密码(substitution cipher): 利用一种东西替代另一种东西

凯撒密码：一个字母替代另一个字母
将一个字母利用字母表中该字母后面的第k个字母替代
如k=3，bob. i love you. alice → ere, l oryh brx. dolfh
单码(字母)替代密码：26个字母集合向26个字母集合的映射
明文:abcdefghijklmnopqrstuvwxyz
密文:mnbvcxzasdfghjklpoiuytrewq
明文: bob. i love you. alice
密文: nkn. s gktc wky. mgsbc
多码(字母)替代加密:使用多个单码替代密码，明文中不同位置的字母使用不同的单码替代密码
例如，使用采用两个凯撒密码的多码替代加密:
加密秘钥: (C1=5, C2=19); C1, C2, C2, C1, C2 ……
明文: bob. i love you.
密文: ghu. n etox dhz.
C1(k=5) :使用该字母后面的第 5个字母替代
C2(k=19):使用该字母后面的第19个字母替代
C1, C2, C2, C1, C2 …… 代表了明文中字符替换使用的规则，如第一个字符采用C1，第二个字符采用C2,第三个字符采用C2….
C1与C2 与 C1,C2,C2 … 这个串，共同构成了密码本

换位密码(transpositions): 重新排列明文中的字母

置换法(permutation method)
将明文划分为固定长度(d)的组，每个组内的字母按置换规则 (f)变换位置
密钥:(d, f) 例如:
秘钥: d=4, f:=(1→3, 2→1, 3→4, 4→2) 每组长度4 每组的第1个字符放在第3个位置，第2个字符放在第1个位置，。。。

明文(m): i love you.
分组: ilov eyou
密文(c): lvio yueo
列置换加密将明文按行组成一个矩阵，然后按给定列顺序输出得到密文
例如:
秘钥: k=4(矩阵列数), (2, 3, 1, 4)(输出顺序)
明文(m): bob. i love you.
密文(c): ooo bvu bly iex

变换规则如图所示：
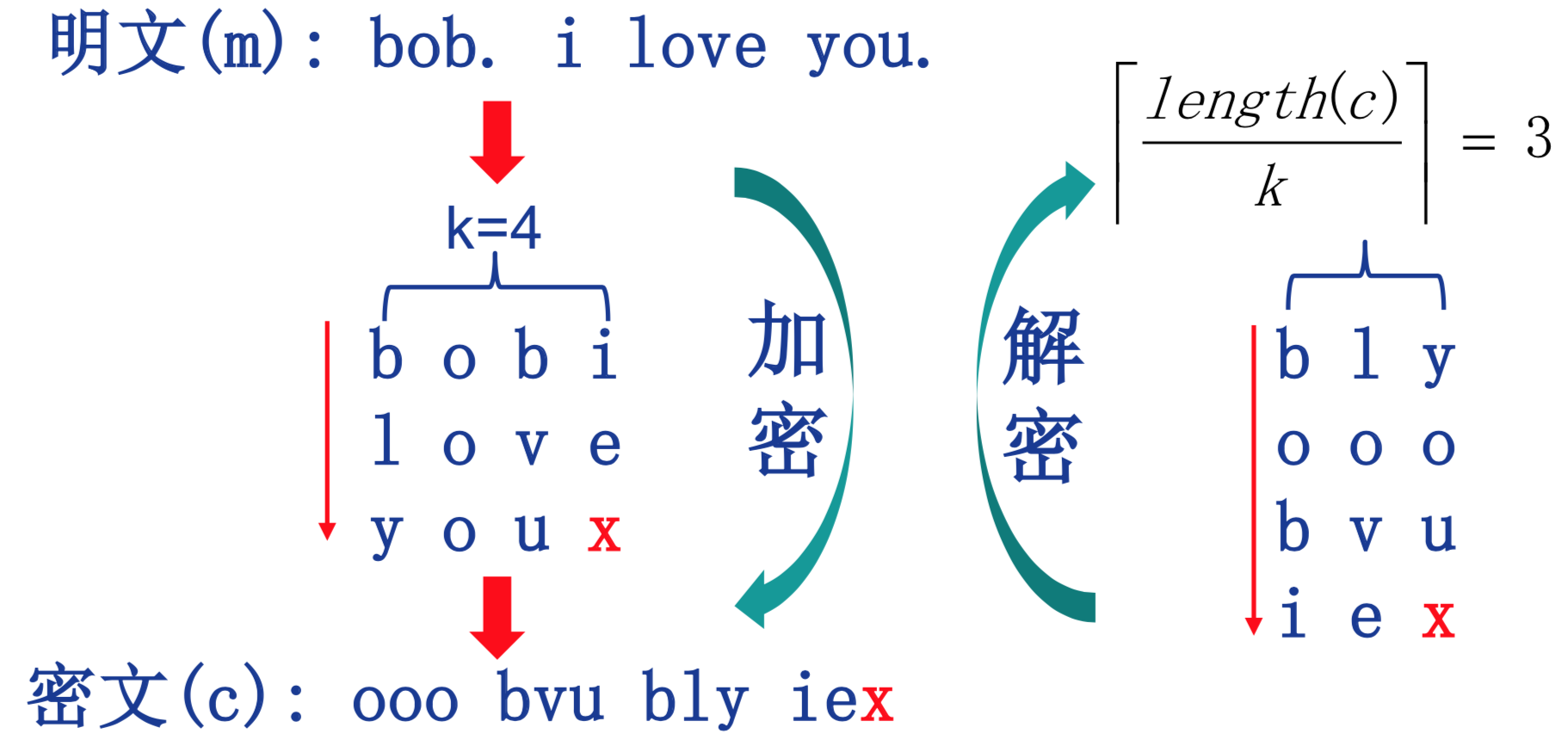
列置换加密的密钥包括列数和输出顺序
可以用一个单词来表示单词长度表示列数，单词中的字母顺序表示输出顺序
例如: 秘钥: nice
明文(m): bob. i love you.
密文(c): bvu iex ooo bly

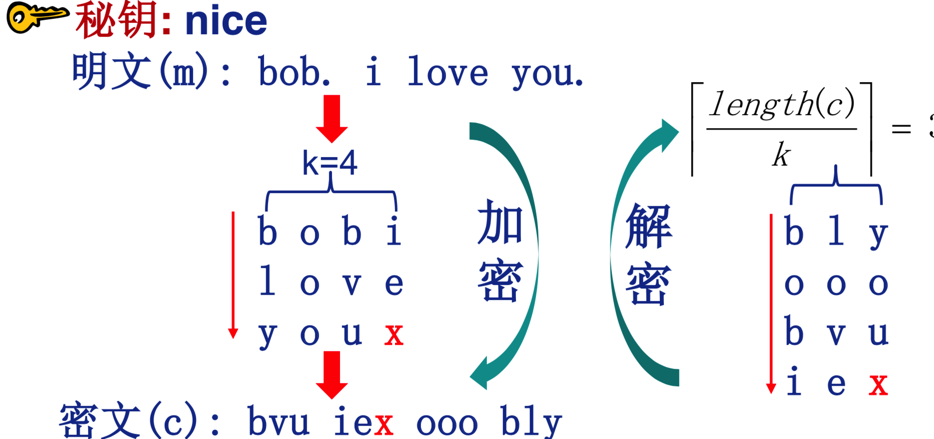
现代加密技术的基本操作包括经典的替代和置换，但是不再针对一个个字母，而是针对二进制位操作

现代加密技术主要分为:
对称密钥加密 DES、 3DES、 AES
非对称密钥加密(公开密钥加密) RSA

对称密钥加密:
需要发送方与接收方知道共享的秘密密钥

流密码(stream ciphers)
- 首先利用密钥K产生一个密钥流:z=z0 z1 z2 …
- 然后使用如下规则对明文串x=x0x1x2…加密:y=y0y1y2…=Ez0(x0)Ez1(x1)Ez2(x2)…
- 解密时，使用相同的密钥流与密文做运算 (XOR)
分组密码，也称块密码(block ciphers)
将明文序列划分成长为m的明文组，各明文组在长为i的密钥组的控制下变换成长度为n的密文组
通常取n=m
n>m 扩展分组密码
n<m 压缩分组密码

在设计密码体制的过程中，Shannon提出了能够破坏对密码系统进行各种统计分析攻击的两个基本操作: 扩散(diffusion)和混淆(confusion)基于1949年Shannon提出的交替使用替代和置换方式构造密码体制。

非对称秘钥加密
发送方与接收方无需共享秘密密钥
公开密钥(公钥)完全公开
私有密钥(私钥)只有接收方知道

基于“扩散”和“混乱”的思考，Feistel提出通过替代和置换交替操作方式构造密码Feistel是一种设计原则，并非一个特殊的密码。流程图大致如下

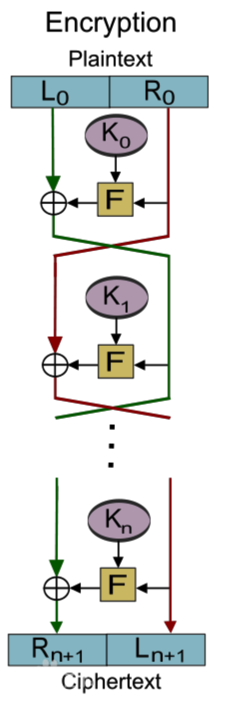
加密过程:
将明文分成左、右两部分:
明文 = (L0, R0)
每一轮i=1, 2 , … , n计算:
Li= Ri-1 Ri= Li-1 xor (Ri-1, Ki)
其中F是轮函数; Ki是子密钥
密文 = (Ln, Rn)

解密过程: 密文 = (Ln,Rn)
每一轮i=n, n-1, … , 1计算:
Ri-1 = Li
Li-1 = Ri xor F(Ri-1,Ki) 其中F是轮函数; Ki是子密钥
明文 = (L0, R0)

Feistel结构的分组密码安全性取决于:

行者常至，为者常成！