目录
树形结构
生活中的树形结构
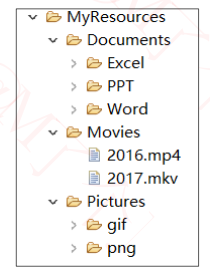
使用树形结构可以大大提高效率
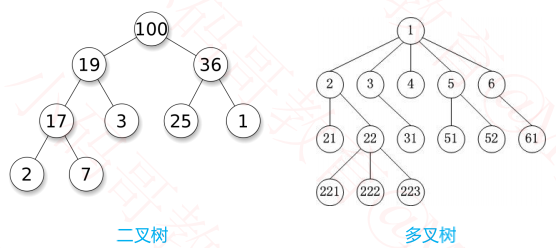
一、树的基本概念
1、节点
按节点位置:根节点、父节点、子节点、兄弟节点
按节点的度:叶子节点(度为0的节点)、非叶子节点(度不为0的节点)
节点的度(degree):子树的个数
节点的深度(depth):从根节点到当前节点的唯一路径上的节点总数
节点的高度(height):从当前节点到最远叶子节点的路径上的节点总数
2、树
子树、左子树、右子树
空树:没有任何节点的树
有序树:树中任意节点的子节点之间有顺序关系
无序树:树中任意节点的子节点之间没有顺序关系,也称为“自由树”
森林:由 m(m ≥ 0)棵互不相交的树组成的集合
树的度:所有节点度中的最大值
树的深度:所有节点深度中的最大值
树的高度:所有节点高度中的最大值
树的深度 等于 树的高度
层数(level):根节点在第 1 层,根节点的子节点在第 2 层,以此类推(有些教程也从第 0 层开始计算)
二叉树
一、二叉树的特点
二叉树的特点:每个节点的度最大为 2(最多拥有 2 棵子树)
左子树和右子树是有顺序的:即使某节点只有一棵子树,也要区分左右子树
二叉树是有序树
二、二叉树的性质
非空二叉树的第 i 层,最多有 2^(i − 1) 个节点( i ≥ 1 )
在高度为 h 的二叉树上最多有 2^h − 1 个结点( h ≥ 1 )
对于任何一棵非空二叉树,如果叶子节点个数为 n0,度为 2 的节点个数为 n2,则有: n0 = n2 + 1
总结点n = n0+n1+n2;
总边数T = n1 + 2*n2;
总结点n = T+1;
因此 n0 = n2 + 1
三、真二叉树(Proper Binary Tree)
所有节点的度都要么为 0,要么为 2
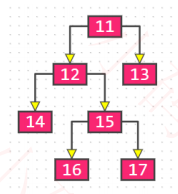
四、满二叉树(Full Binary Tree)
满二叉树:所有节点的度都要么为 0,要么为 2。且所有的叶子节点都在最后一层
所以满二叉树一定是真二叉树,而真二叉树不一定是满二叉树。
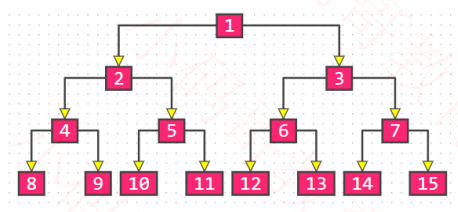
假设满二叉树的高度为 h( h ≥ 1 ),那么
第 i 层的节点数量: 2^(i − 1)
叶子节点数量: 2^(h − 1)
总节点数量 n = 2^0 + 2^1 + 2^2 + ⋯ + 2^(h−1) = 2^h − 1
h = log2^(n + 1)
在同样高度的二叉树中,满二叉树的叶子节点数量最多、总节点数量最多
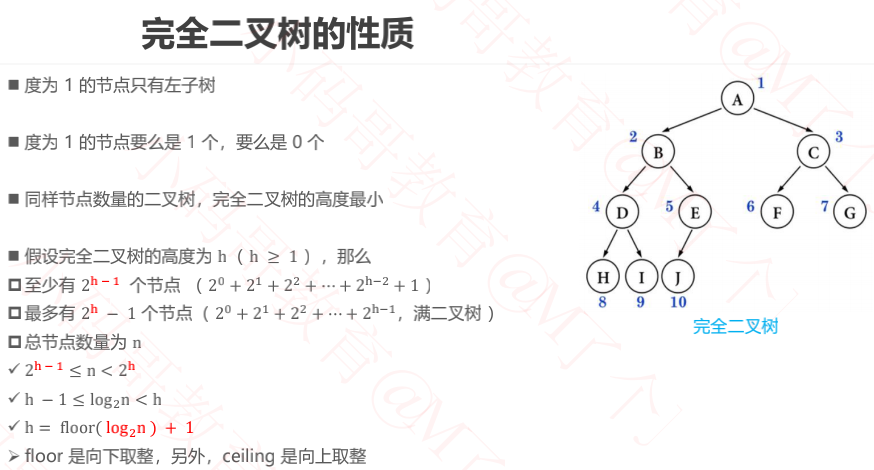
五、完全二叉树(Complete Binary Tree)
1、完全二叉树
完全二叉树:叶子节点只会出现最后 2 层,且最后 1 层的叶子结点都靠左对齐
满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
完全二叉树从根结点至倒数第 2 层是一棵满二叉树

总结:完全二叉树就是按顺序进行码放,中间没有空余。
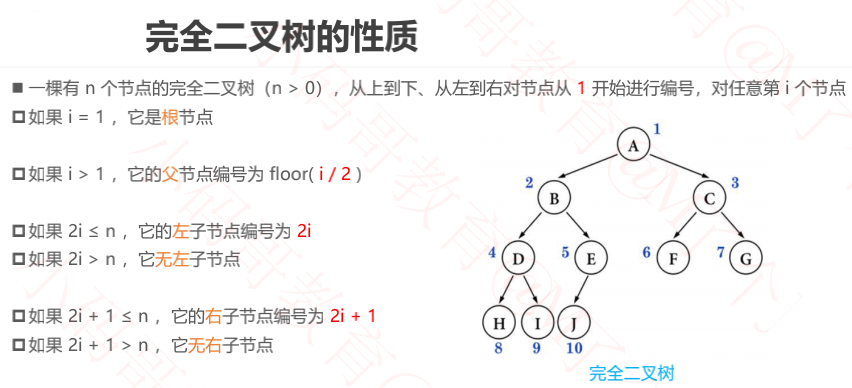
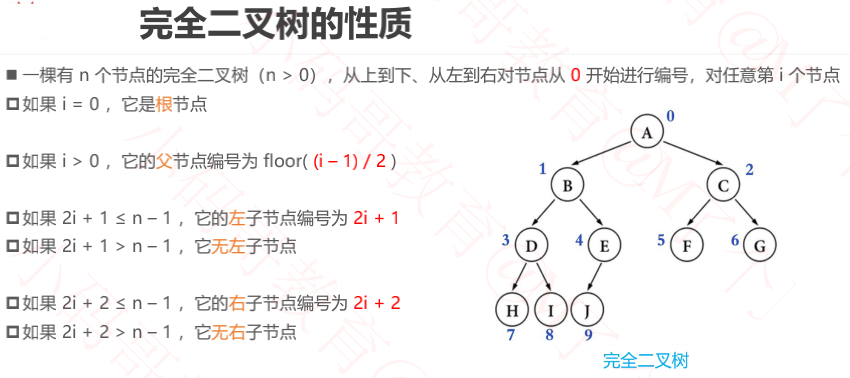
2、完全二叉树的性质
六、看一道题

二叉搜索树
一、思考
◼ 在 n 个动态的整数中搜索某个整数?(查看其是否存在)
◼ 假设使用动态数组存放元素,从第 0 个位置开始遍历搜索,平均时间复杂度:O(n)

◼ 如果维护一个有序的动态数组,使用二分搜索,最坏时间复杂度:O(logn)
◼ 但是添加、删除的平均时间复杂度是 O(n)

◼ 针对这个需求,有没有更好的方案?
◼ 使用二叉搜索树,添加、删除、搜索的最坏时间复杂度均可优化至:O(logn)
二、二叉搜索树
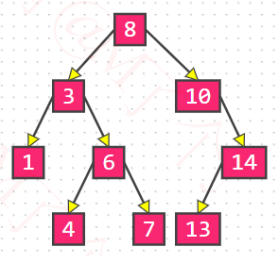
1、二叉搜索树是二叉树的一种,是应用非常广泛的一种二叉树,英文简称为 BST。又被称为:二叉查找树、二叉排序树
任意一个节点的值都大于其左子树所有节点的值
任意一个节点的值都小于其右子树所有节点的值
它的左右子树也是一棵二叉搜索树
2、二叉搜索树可以大大提高搜索数据的效率
3、二叉搜索树存储的元素必须具备可比较性
比如 int、double 等
如果是自定义类型,需要指定比较方式
不允许为 null
三、二叉搜索树的接口设计
◼ int size() // 元素的数量
◼ boolean isEmpty() // 是否为空
◼ void clear() // 清空所有元素
◼ void add(E element) // 添加元素
◼ void remove(E element) // 删除元素
◼ boolean contains(E element) // 是否包含某元素
◼ 需要注意的是
对于我们现在使用的二叉树来说,它的元素没有索引的概念
为什么?
四、添加节点
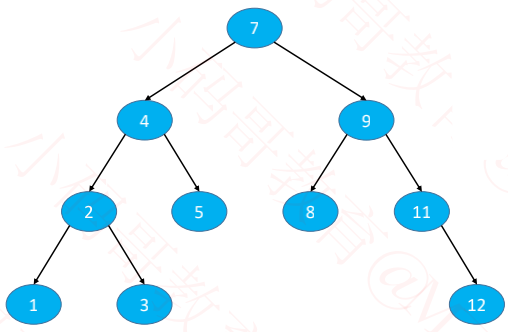
◼ 比如添加12、1
◼ 添加步骤
找到父节点 parent
创建新节点 node
parent.left = node 或者 parent.right = node
◼ 遇到值相等的元素该如何处理?
建议覆盖旧的值
六、元素的比较方案设计
-
允许外界传入一个 Comparator 自定义比较方案
-
如果没有传入 Comparator,强制认定元素实现了 Comparable 接口
行者常至,为者常成!
