目录
二叉树遍历
遍历是数据结构中的常见操作,把所有元素都访问一遍
线性数据结构的遍历比较简单
正序遍历
逆序遍历
根据节点访问顺序的不同,二叉树的常见遍历方式有4种
前序遍历(Preorder Traversal)
中序遍历(Inorder Traversal)
后序遍历(Postorder Traversal)
层序遍历(Level Order Traversal)
一、前序遍历
访问顺序
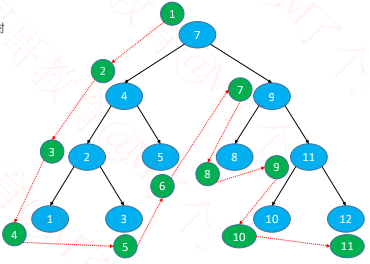
根节点、前序遍历左子树、前序遍历右子树
7、4、2、1、3、5、9、8、11、10、12
二、中序遍历
访问顺序
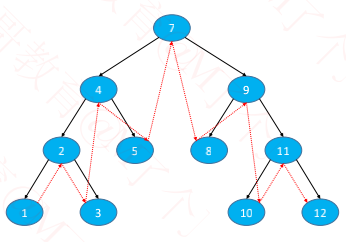
中序遍历左子树、根节点、中序遍历右子树
1、2、3、4、5、7、8、9、10、11、12
如果访问顺序是下面这样呢?
中序遍历右子树、根节点、中序遍历左子树
12、11、10、9、8 、7、5、4、3、2、1
二叉搜索树的中序遍历结果是升序或者降序取决于遍历书序:
升序:左子树、根节点、右子树
降序:右子树、根节点、左子树
三、后续遍历
访问顺序
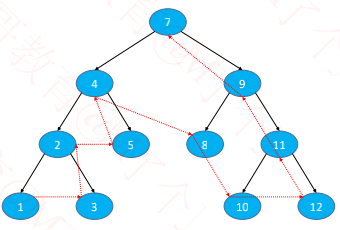
后序遍历左子树、后序遍历右子树、根节点
1、3、2、5、4、8、10、12、11、9、7
四、层序遍历
访问顺序
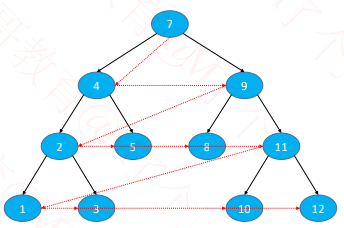
从上到下、从左到右依次访问每一个节点
7、4、9、2、5、8、11、1、3、10、12
实现思路:使用队列
-
将根节点入队
-
循环执行以下操作,直到队列为空
将队头节点 A 出队,进行访问
将 A 的左子节点入队
将 A 的右子节点入队
二叉树遍历应用
前序遍历
树状结构展示(注意左右子树的顺序)
中序遍历
二叉搜索树的中序遍历按升序或者降序处理节点
后序遍历
适用于一些先子后父的操作
层序遍历
计算二叉树的高度
判断一棵树是否为完全二叉树
根据遍历结果重构二叉树
以下结果可以保证重构出唯一的一棵二叉树
前序遍历 + 中序遍历
后序遍历 + 中序遍历
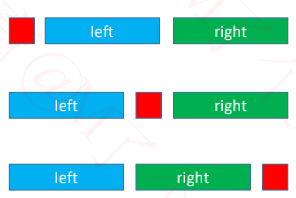
前序遍历 + 后序遍历
✓ 如果它是一棵真二叉树(Proper Binary Tree),结果是唯一的
✓ 不然结果不唯一

前序遍历+中序遍历重构二叉树
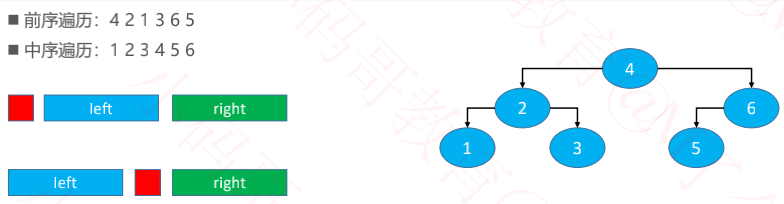
遍历相关练习
一、反转二叉树
1、层序遍历方式
语言:c++
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(!root) return root;
queue<TreeNode*>* tququ = new queue<TreeNode*>();
tququ->push(root);
while (tququ->size()) {
TreeNode * topNode = tququ->front();
tququ->pop();
TreeNode * temp = topNode->left;
topNode->left = topNode->right;
topNode->right = temp;
if (topNode->left) {
tququ->push(topNode->left);
}
if (topNode->right) {
tququ->push(topNode->right);
}
}
delete tququ;
return root;
}
};
2、同样也可以采用前序、中序、后序遍历的方式来实现
二、计算树的高度
1、recursion递归方式
语言:OC
/// 计算二叉树的高度
-(int)_heightByRecursion:(LCBTNode*)node{
if(!node) return 0;
int leftHeight = [self _heightByRecursion:node->_left];
int rightHeight = [self _heightByRecursion:node->_right];
return leftHeight>rightHeight?leftHeight+1:rightHeight+1;
}
2、层序遍历方式
语言:OC
-(int)heightByLevelorder{
int height = 0;
if(!_root) return height;
int currentLevelSize = 1;
self.queue->push(_root);
while (self.queue->size()) {
LCBTNode * topNode = self.queue->front();
self.queue->pop();
currentLevelSize--;
//对节点进行处理
if (topNode->_left) {
self.queue->push(topNode->_left);
}
if (topNode->_right) {
self.queue->push(topNode->_right);
}
//当currentLevelSize为0时,表明
//当前层的所有节点都从队列移除
//下一层的所有节点都已进入队列
if (currentLevelSize == 0) {
//记录下一层的节点数量
currentLevelSize = (int)self.queue->size();
//当前层结束,层高+1
height++;
}
}
return height;
}
三、判断是否为完全二叉树
如果树为空,返回 false
如果树不为空,开始层序遍历二叉树(用队列)
如果 node.left!=null,将 node.left 入队
如果 node.left==null && node.right!=null,返回 false
如果 node.right!=null,将 node.right 入队
如果 node.right==null
✓ 那么后面遍历的节点应该都为叶子节点,才是完全二叉树
✓ 否则返回 false
遍历结束,返回 true
-(BOOL)isComplete{
if(!_root) return false;
BOOL isLeaf = false;
self.queue->push(_root);
while (!self.queue->empty()) {
LCBTNode * topNode = self.queue->front();
self.queue->pop();
//对节点进行处理
if (isLeaf &&(topNode->_left || topNode->_right)) return false;
if (topNode->_left && topNode->_right){//都不为空就入队列
self.queue->push(topNode->_left);
self.queue->push(topNode->_right);
}else if (topNode->_left && !topNode->_right){//左边不为空右边为空 后面全是叶子节点
isLeaf = true;
}else if (!topNode->_left && topNode->_right){//左边为空右边不为空,返回false
return false;
}else if (!topNode->_left && !topNode->_right){//都为空 后面全是叶子节点
isLeaf = true;
};
}
self.queue = nil;
return true;
}
前驱与后继节点
一、前驱节点
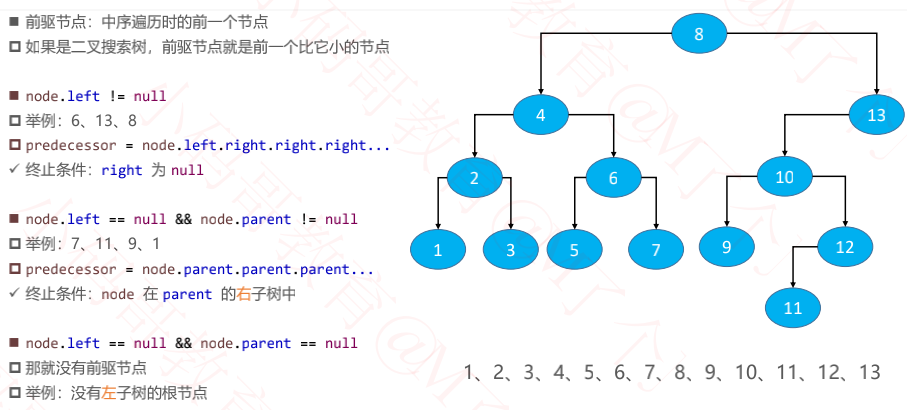
/// 获取前驱节点
-(LCBTNode*)predecessor:(LCBTNode*)node{
if(!node) return nil;
LCBTNode * predeNode = node->_left;
//如果左节点存在
if (predeNode) {
while (predeNode->_right) {
predeNode = predeNode->_right;
}
return predeNode;
}
//如果左节点不存在
while (node->_parent && node != node->_parent->_right) {
node = node->_parent;
}
return node->_parent;
}
二、后继节点
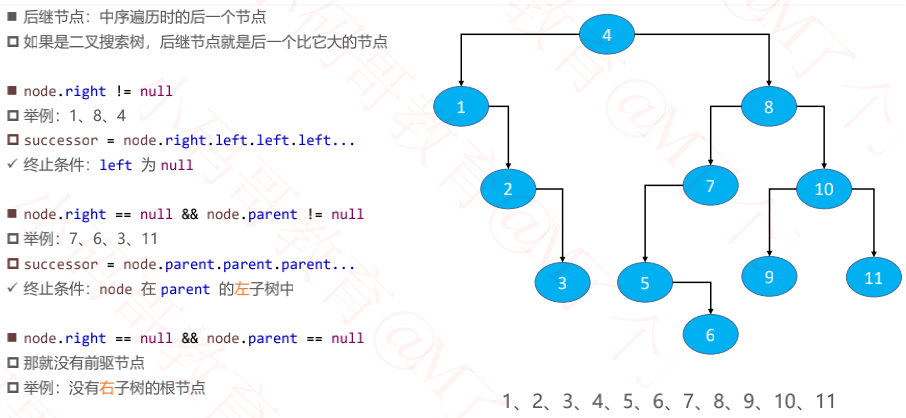
//获取后继节点
-(LCBTNode*)successor:(LCBTNode*)node{
if(!node) return nil;
LCBTNode * predeNode = node->_right;
//如果左节点存在
if (predeNode) {
while (predeNode->_left) {
predeNode = predeNode->_left;
}
return predeNode;
}
//如果左节点不存在
while (node->_parent && node != node->_parent->_left) {
node = node->_parent;
}
return node->_parent;
}
行者常至,为者常成!
