目录
二叉树删除
一、删除叶子节点
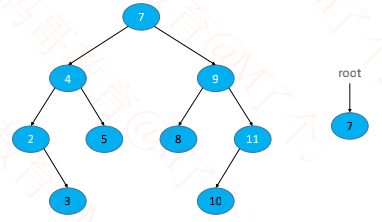
◼ 直接删除
node == node.parent.left
✓ node.parent.left = null
node == node.parent.right
✓ node.parent.right = null
node.parent == null
✓ root = null
二、删除度为1的节点
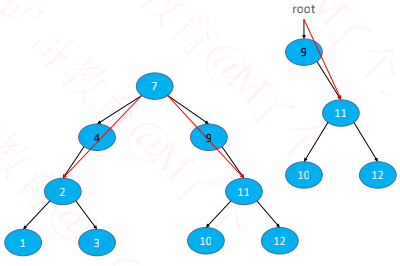
child 是 node.left 或者 child 是 node.right
用 child 替代 node 的位置
✓ 如果 node 是左子节点
➢ child.parent = node.parent
➢ node.parent.left = child
✓ 如果 node 是右子节点
➢ child.parent = node.parent
➢ node.parent.right = child
✓ 如果 node 是根节点
➢ root = child
➢ child.parent = null
三、删除度为2的节点
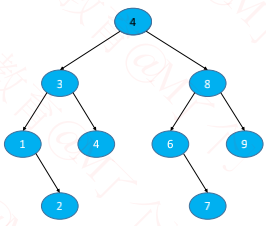
◼ 举例:先删除 5、再删除 4
◼ 先用前驱或者后继节点的值覆盖原节点的值
◼ 然后删除相应的前驱或者后继节点
◼ 如果一个节点的度为 2,那么
它的前驱、后继节点的度只可能是 1 和 0
四、代码实现
-(void)__removeNode:(LCBTNode*)node{
if(!node) return;
_size--;
/**
删除度为2的节点策略:
对于二叉搜索树删除度为2的节点,应该找到其前驱或后继节点来顶替被删除的节点。
因为前驱或后继节点在中序排序中是紧挨着被删除节点的,这样不会破坏二叉搜索树的性质
*/
if ([node degree] == 2) {//度为2的节点
//找到后继节点(因为度为2,后继节点一定存在)
LCBTNode * s = [self __successor:node];
//将当前要删除的节点内容替换为后继节点内容
node->_element = s->_element;
/**
重要:度为2的节点的前驱节点和后继节点的度一定为1或者0,不可能为2;
所以删除一个度为2的节点就转化为了删除一个度为1或者0的节点。
*/
//删除当前节点转化为删除后继节点
node = s;
}
LCBTNode* replaceNode = node->_left?node->_left:node->_right;
if (replaceNode) {//replaceNode存在,node是度为1的节点
replaceNode->_parent = node->_parent;
if (!node->_parent) {//node是根节点
_root = replaceNode;
}else if(node == node->_parent->_left){
node->_parent->_left = replaceNode;
}else{
node->_parent->_right = replaceNode;
}
}else{//replaceNode为空,node是度为0的节点(叶子节点)
if (!node->_parent) {//node是根节点
_root = nil;
}else if(node == node->_parent->_left){
node->_parent->_left = nil;
}else{
node->_parent->_right = nil;
}
}
}
平衡二叉搜索树BBST(Balanced Binary Search Tree)
一、复杂度分析
1、如果是按照 7、4、9、2、5、8、11 的顺序添加节点
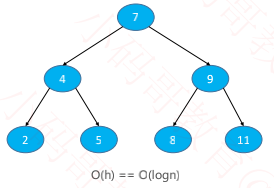
2、如果是从小到大添加节点
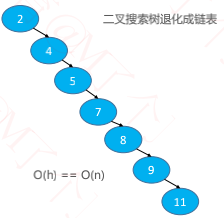
◼ 当 n 比较大时,两者的性能差异比较大
◼ 比如 n = 1000000 时,二叉搜索树的最低高度是 20
二、退化成链表的另一种情况
删除节点时也可能会导致二叉搜索树退化成链表
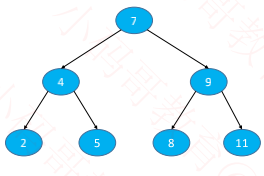
其实,添加、删除节点时,都可能会导致二叉搜索树退化成链表
有没有办法防止二叉搜索树退化成链表?
让添加、删除、搜索的复杂度维持在 O(logn)
三、平衡
1、平衡:当节点数量固定时,左右子树的高度越接近,这棵二叉树就越平衡(高度越低)
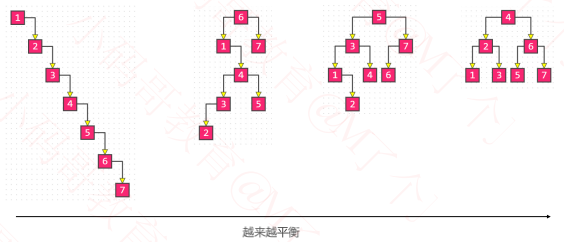
2、理想平衡:最理想的平衡,就是像完全二叉树、满二叉树那样,高度是最小的
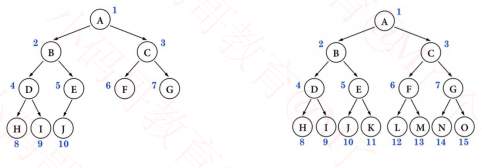
四、如何改进二叉搜索树
◼ 首先,节点的添加、删除顺序是无法限制的,可以认为是随机的
◼ 所以,改进方案是:在节点的添加、删除操作之后,想办法让二叉搜索树恢复平衡(减小树的高度)
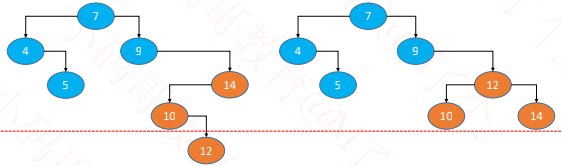
◼ 如果接着继续调整节点的位置,完全可以达到理想平衡,但是付出的代价可能会比较大
比如调整的次数会比较多,反而增加了时间复杂度
◼ 总结来说,比较合理的改进方案是:用尽量少的调整次数达到适度平衡即可
◼ 一棵达到适度平衡的二叉搜索树,可以称之为:平衡二叉搜索树
五、常见平衡二叉搜索树
1、AVL树
✓ Windows NT 内核中广泛使用
2、红黑树
✓ C++ STL(比如 map、set )
✓ Java 的 TreeMap、TreeSet、HashMap、HashSet
✓ Linux 的进程调度
✓ Ngix 的 timer 管理
一般也称它们为:自平衡的二叉搜索树(Self-balancing Binary Search Tree)
行者常至,为者常成!
