目录
上楼梯
楼梯有 n 阶台阶,上楼可以一步上 1 阶,也可以一步上 2 阶,走完 n 阶台阶共有多少种不同的走法?
假设 n 阶台阶有 f(n) 种走法,第 1 步有 2 种走法
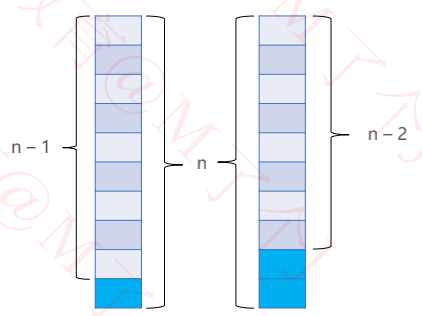
✓ 如果上 1 阶,那就还剩 n – 1 阶,共 f(n – 1) 种走法
✓ 如果上 2 阶,那就还剩 n – 2 阶,共 f(n – 2) 种走法
所以 f(n) = f(n – 1) + f(n – 2)
/// 上n阶楼梯有多少种走法
/// @param n n阶
-(int)climbStairs:(int)n{
if (n<=2) return n;
return [self climbStairs:n-1] + [self climbStairs:n-2];
}
跟斐波那契数列几乎一样,因此优化思路也是一致的
/// 上n阶楼梯有多少种走法
/// @param n n阶
-(int)climbStairs2:(int)n{
if (n<=2) return n;
int first = 1;
int second = 2;
for (int i = 3; i<=n; i++) {
second = second + first;
first = second - first;
}
return second;
}
汉诺塔(Hanoi)
一、问题描述
编程实现把 A 的 n 个盘子移动到 C(盘子编号是 [1, n] )
每次只能移动1个盘子
大盘子只能放在小盘子下面

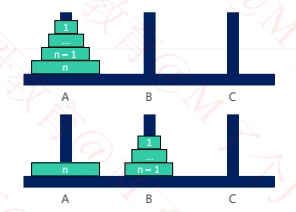
二、示例演示

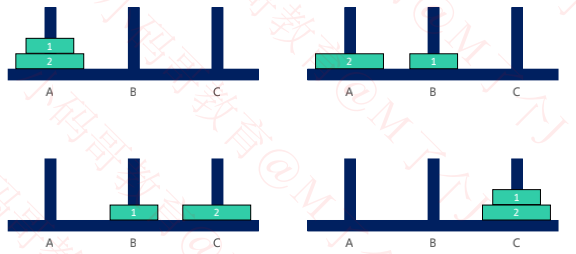
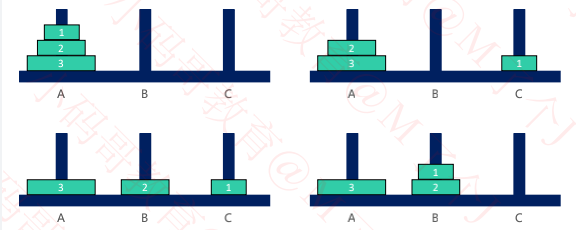
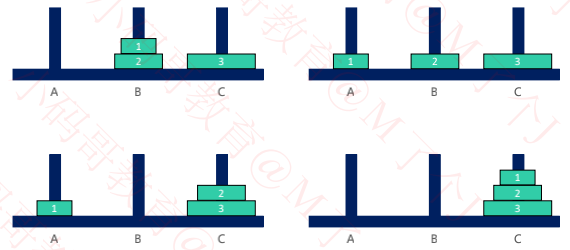
三、思路及实现
其实分 2 种情况讨论即可
当 n == 1时,直接将盘子从 A 移动到 C
当 n > 1时,可以拆分成3大步骤
① 将 n – 1 个盘子从 A 移动到 B
② 将编号为 n 的盘子从 A 移动到 C
③ 将 n – 1 个盘子从 B 移动到 C
步骤 ① ③ 明显是个递归调用

/// 将n个碟子从p1移动到p3,p2作为辅助柱子
/// @param n 碟子个数
/// @param p1 柱子1
/// @param p2 柱子2
/// @param p3 柱子3
-(void)hanoiWithN:(int)n
pillar1:(NSString*)p1
pillar2:(NSString*)p2
pillar3:(NSString*)p3{
if (n==1) {
[self __move:1 from:p1 to:p3];
return;
}
[self hanoiWithN:n-1 pillar1:p1 pillar2:p3 pillar3:p2];
[self __move:n from:p1 to:p3];
[self hanoiWithN:n-1 pillar1:p2 pillar2:p1 pillar3:p3];
}
/// 移动第n号盘子从from到to
/// @param n 第n号
/// @param from 起始柱子
/// @param to 终止柱子
-(void)__move:(int)n from:(NSString*)from to:(NSString*)to{
NSLog(@"%d号:%@ -> %@",n,from,to);
}
T n = 2 ∗ T n − 1 + O(1)
因此时间复杂度是:O 2n
空间复杂度:O n
递归转非递归
一、
递归调用的过程中,会将每一次调用的参数、局部变量都保存在了对应的栈帧(Stack Frame)中
[self.recursion log:4];
-(void)log:(int)n{
if (n<1) return;
[self log:n-1];
int v = n + 10;
NSLog(@"log:%d",v);
}
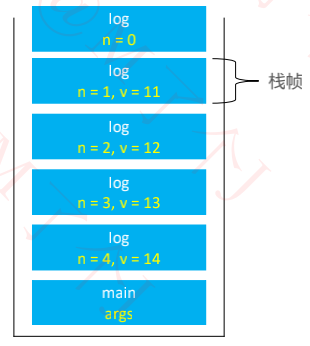
若递归调用深度较大,会占用比较多的栈空间,甚至会导致栈溢出
在有些时候,递归会存在大量的重复计算,性能非常差
这时可以考虑将递归转为非递归(递归100%可以转换成非递归)
二、
递归转非递归的万能方法
自己维护一个栈,来保存参数、局部变量
但是空间复杂度依然没有得到优化
-(void)log2:(int)n{
stack<LCFrame*> frameStack;
while (n) {
LCFrame * frame = [LCFrame frameWithN:n v:n+10];
frameStack.push(frame);
n--;
}
while (frameStack.size()) {
LCFrame * topFrame = frameStack.top();
frameStack.pop();
NSLog(@"log:%d",topFrame.v);
}
}
三、
在某些时候,也可以重复使用一组相同的变量来保存每个栈帧的内容
-(void)log3:(int)n{
for (int i= 1; i<=n; i++) {
NSLog(@"log:%d",i+10);
}
}
这里重复使用变量 i 保存原来栈帧中的参数
空间复杂度从 O(n) 降到了 O(1)
尾调用
一、尾调用
尾调用:一个函数的最后一个动作是调用函数
-(void)test1{
int a = 10;
int b = a + 20;
[self test2:b];
}
如果最后一个动作是调用自身,称为尾递归(Tail Recursion),是尾调用的特殊情况
-(void)test2:(int)n{
if (n<0) return;
[self test2:n-1];
}
一些编译器能对尾调用进行优化,以达到节省栈空间的目的
下面代码不是尾调用
-(int)factorial:(int)n{
if (n<=1) return n;
return n*[self factorial:n-1];
}
因为它最后1个动作是乘法
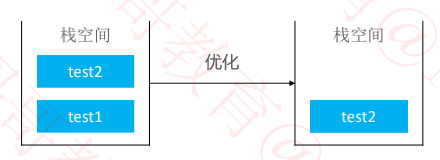
二、尾调用优化
尾调用优化也叫做尾调用消除(Tail Call Elimination) 如果当前栈帧上的局部变量等内容都不需要用了,当前栈帧经过适当的改变后可以直接当作被尾调用的函数的栈帧使用,然后程序可以 jump 到被尾调用的函数代码
生成栈帧改变代码与 jump 的过程称作尾调用消除或尾调用优化
尾调用优化让位于尾位置的函数调用跟 goto 语句性能一样高
消除尾递归里的尾调用比消除一般的尾调用容易很多
比如Java虚拟机(JVM)会消除尾递归里的尾调用,但不会消除一般的尾调用(因为改变不了栈帧)
因此尾递归优化相对比较普遍,平时的递归代码可以考虑尽量使用尾递归的形式
void test(int n){
if (n<0) return;
printf("n - %d\n",n);
test(n-1);
}

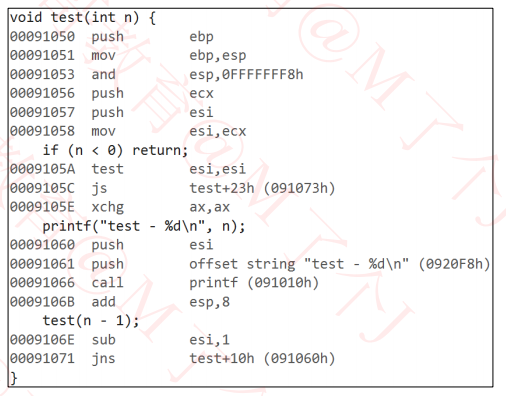
三、尾递归示例1
求 n 的阶乘 123…(n-1)*n (n>0)
优化前
-(int)factorial:(int)n{
if (n<=1) return n;
return n*[self factorial:n-1];
}
优化后
//尾调用
-(int)factorial2:(int)n{
return [self factorial2:n result:1];
}
//每个调用栈的返回值 都是n=1时返回的result
-(int)factorial2:(int)n result:(int)result{
if (n <= 1) return result;
return [self factorial2:n-1 result:n*result];
}
画一画调用栈可知:
结果result,是从栈顶(n=1)开始,一路返回到栈底(n=n)。尾递归是将 要得到的结果 一直累积到栈顶,在最后一次返回
四、尾递归示例2
斐波那契数列
优化前
//非尾递归
-(int)fibTest:(int)n{
if (n<=2) return 1;
return [self fibTest:n-1] + [self fibTest:n-2];
}
优化后
//尾递归
-(int)fibTest2:(int)n{
return [self fibTest2:n first:1 second:1];
}
-(int)fibTest2:(int)n first:(int)first second:(int)second{
if (n<=2) return second;
return [self fibTest2:n-1 first:second second:first+second];
}
行者常至,为者常成!
