目录
递归介绍
一、递归现象
从前有座山,山里有座庙,庙里有个老和尚,正在给小和 尚讲故事呢!故事是什么呢?【从前有座山,山里有座庙, 庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢? 『从前有座山,山里有座庙,庙里有个老和尚,正在给小 和尚讲故事呢!故事是什么呢?……』】
GNU 是 GNU is Not Unix 的缩写
GNU → GNU is Not Unix → GNU is Not Unix is Not Unix → GNU is Not Unix is Not Unix is Not Unix
假设A在一个电影院,想知道自己坐在哪一排,但是前面人很多,
A 懒得数,于是问前一排的人 B【你坐在哪一排?】,只要把 B 的答案加一,就是 A 的排数。
B 懒得数,于是问前一排的人 C【你坐在哪一排?】,只要把 C 的答案加一,就是 B 的排数。
C 懒得数,于是问前一排的人 D【你坐在哪一排?】,只要把 D 的答案加一,就是 C 的排数。
……
直到问到最前面的一排,最后大家都知道自己在哪一排了
二、递归调用
递归:函数(方法)直接或间接调用自身。是一种常用的编程技巧
直接调用
/// 递归求和(调用自身)
/// @param n n
-(int)sum:(int)n{
if (n<=1) return 1;
return n+[self sum:n-1];
}
间接调用
/// 间接调用演示
/// @param n n
-(void)indirectA:(int)n{
NSLog(@"n = %d",n);
if (n<0) return;
[self indirectB:n];
}
-(void)indirectB:(int)n{
[self indirectA:--n];
}
三、函数的递归调用过程
1、函数的调用过程
void main(char* args[] ){
test1(10);
test2(20);
}
void test1(int v){ }
void test2(int v){
test3(30);
}
void test3(int v){ }
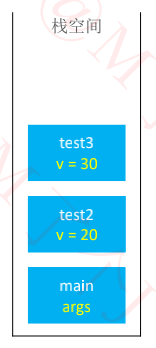
2、函数的递归调用过程
void main(int argv,char* args[] ){
sum(4);
}
int sum(int n){
if (n<=1) return n;
return n+sum(n-1);
}
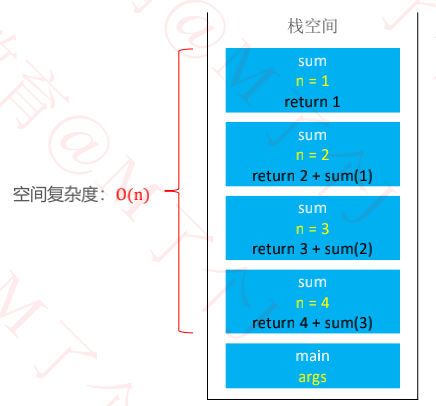
空间复杂度:O(n)
如果递归调用没有终止,将会一直消耗栈空间
最终导致栈内存溢出(Stack Overflow)
所以必需要有一个明确的结束递归的条件
也叫作边界条件、递归基

四、示例分析
求 1+2+3+…+(n-1)+n 的和(n>0)
/// 递归求和(调用自身)
/// @param n n
-(int)sum:(int)n{
if (n<=1) return 1;
return n+[self sum:n-1];
}
总消耗时间 T(n) = T(n − 1) + O(1),因此
时间复杂度:O(n)
空间复杂度:O(n)
/// 求和优化1(迭代)
/// @param n n
-(int)sum1:(int)n{
int sum = 0;
for (int i = 1; i<=n; i++) {
sum+=i;
}
return sum;
}
时间复杂度:O(n),空间复杂度:O(1)
/// 求和优化2
/// @param n n
-(int)sum2:(int)n{
return ((n+1)*n) >> 1;
}
时间复杂度:O(1),空间复杂度:O(1)
注意:
使用递归不是为了求得最优解,是为了简化解决问题的思路,代码会更加简洁
递归求出来的很有可能不是最优解,也有可能是最优解
递归思想
一、递归思想
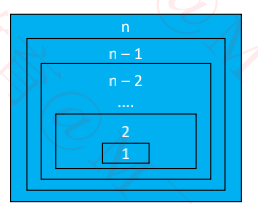
拆解问题
把规模大的问题变成规模较小的同类型问题
规模较小的问题又不断变成规模更小的问题
规模小到一定程度可以直接得出它的解
求解
由最小规模问题的解得出较大规模问题的解
由较大规模问题的解不断得出规模更大问题的解
最后得出原来问题的解
凡是可以利用上述思想解决问题的,都可以尝试使用递归
很多链表、二叉树相关的问题都可以使用递归来解决
因为链表、二叉树本身就是递归的结构(链表中包含链表,二叉树中包含二叉树)
二、使用套路
① 明确函数的功能
先不要去思考里面代码怎么写,首先搞清楚这个函数的干嘛用的,能完成什么功能?
② 明确原问题与子问题的关系
寻找 f(n) 与 f(n – 1) 的关系
③ 明确递归基(边界条件)
递归的过程中,子问题的规模在不断减小,当小到一定程度时可以直接得出它的解
寻找递归基,相当于是思考:问题规模小到什么程度可以直接得出解?
斐波那契数列
斐波那契数列:1、1、2、3、5、8、13、21、34、……
F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n≥3)
编写一个函数求第 n 项斐波那契数
递归实现
/// 返回第n个斐波那契数
/// @param n 第n个
-(int)fib:(int)n{
if (n<=2) return 1;
return [self fib:n-1] + [self fib:n-2];
}
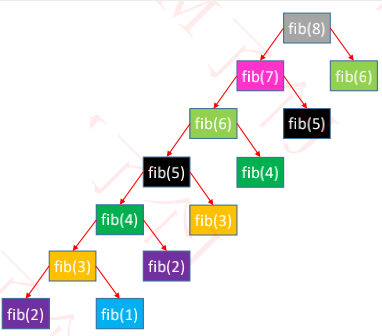
根据递推式 T(n) = T (n − 1) + T(n − 2) + O(1)
可得知时间复杂度:O(2^n)
空间复杂度:O(n)
递归调用的空间复杂度 = 递归深度 * 每次调用所需的辅助空间
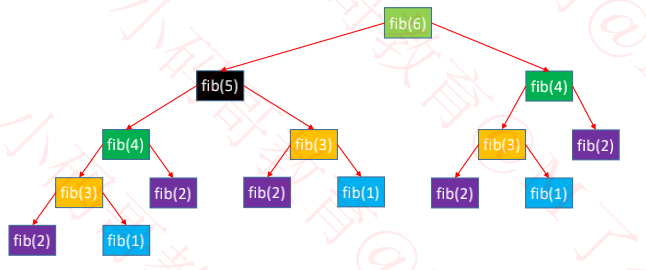
出现了特别多的重复计算
这是一种“自顶向下”的调用过程
一、优化1 - 记忆化
用数组存放计算过的结果,避免重复计算
/// 返回第n个斐波那契数(优化1)
/// @param n 第n个
-(int)fib1:(int)n{
if (n<=2) return 1;
NSMutableArray * nums = [NSMutableArray array];
for (int i= 0; i<=n; i++) {
nums[i] = @(0);
}
nums[1] = nums[2] = @(1);
return [self __fib1:n nums:nums];
}
-(int)__fib1:(int)n nums:(NSMutableArray*)nums{
int num = [nums[n] intValue];
if (num == 0) {
NSLog(@"%d - 未取到值",n);
num = [self __fib1:n-1 nums:nums] + [self __fib1:n-2 nums:nums];
nums[n] = @(num);
}
return num;
}
时间复杂度:O(n),空间复杂度:O(n)
二、优化二 - 去除递归调用
-(int)fib2:(int)n{
if (n<=2) return 1;
NSMutableArray * nums = [NSMutableArray array];
nums[0] = @(0);
nums[1] = @(1);
nums[2] = @(1);
for (int i = 3; i<=n; i++) {
nums[i] = @([nums[i-1] intValue] + [nums[i-2] intValue]);
}
return [nums[n] intValue];
}
时间复杂度:O(n),空间复杂度:O(n)
这是一种“自底向上”的计算过程
三、优化三 - 滚动数组
由于每次运算只需要用到数组中的 2 个元素,所以可以使用滚动数组来优化
-(int)fib3:(int)n{
if (n<=2) return 1;
NSMutableArray * nums = [NSMutableArray array];
nums[0] = @(1);
nums[1] = @(1);
// 3:nums[1] = nums[0] + nums[1]
// nums[0] = @(1);//2
// nums[1] = @(2);//3
//
// 4:nums[0] = nums[0] + nums[1]
// nums[0] = @(3);//4
// nums[1] = @(2);//3
//
// 5:nums[1] = nums[0] + nums[1]
// nums[0] = @(3);//4
// nums[1] = @(5);//5
//
// 6:nums[0] = nums[0] + nums[1]
// nums[0] = @(8);//6
// nums[1] = @(5);//5
for (int i = 3; i<=n; i++) {
nums[i%2] = @([nums[0] intValue] + [nums[1] intValue]);
}
return [nums[n%2] intValue];
}
时间复杂度:O(n),空间复杂度:O(1)
四、优化四 - 位运算取代模运算
乘、除、模运算效率较低,建议用其他方式取代
-(int)fib4:(int)n{
if (n<=2) return 1;
NSMutableArray * nums = [NSMutableArray array];
nums[0] = @(1);
nums[1] = @(1);
for (int i = 3; i<=n; i++) {
nums[i & 1] = @([nums[0] intValue] + [nums[1] intValue]);
}
return [nums[n & 1] intValue];
}
五、优化五
-(int)fib5:(int)n{
int first = 1;
int second = 1;
for (int i = 3; i<=n; i++) {
second = second + first;
first = second - first;
}
return second;
}
时间复杂度:O(n),空间复杂度:O(1)
六、优化六
斐波那契数列有个线性代数解法:特征方程
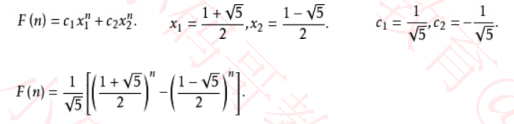
-(int)fib6:(int)n{
double c = sqrt(5.0);//sqrt开平方
return (int)((pow((1+c)/2, n) - pow((1-c)/2, n)) / c);//pow(x,y);x^y
}
时间复杂度、空间复杂度取决于 pow 函数(至少可以低至O(logn) )
行者常至,为者常成!
