目录
Bellman-Ford
一、算法原理
Bellman-Ford 也属于单源最短路径算法,支持负权边,还能检测出是否有负权环
算法原理:对所有的边进行 V – 1 次松弛操作( V 是节点数量),得到所有可能的最短路径
时间复杂度:O(EV) ,E 是边数量,V 是节点数量
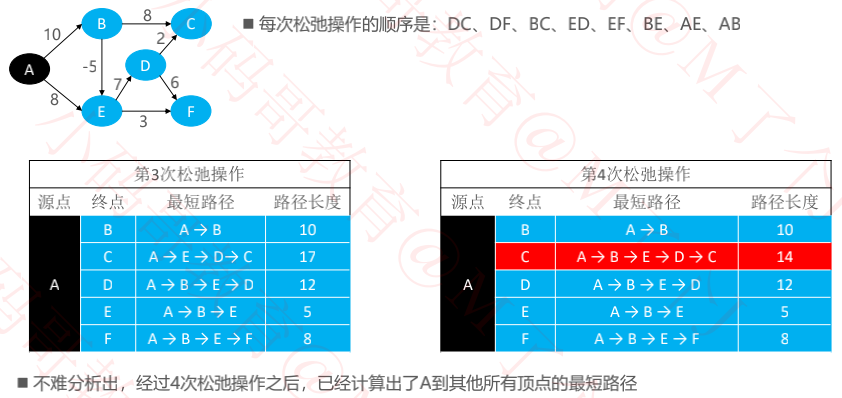
下图的最好情况是恰好从左到右的顺序对边进行松弛操作
对所有边仅需进行 1 次松弛操作就能计算出A到达其他所有顶点的最短路径
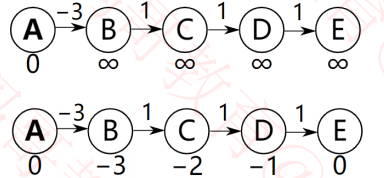
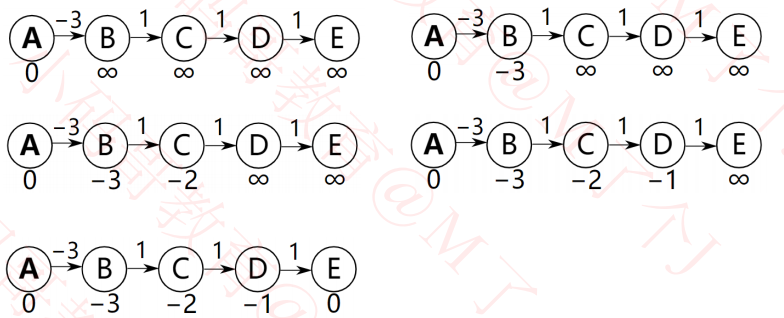
最坏情况是恰好每次都从右到左的顺序对边进行松弛操作
对所有边需进行 V – 1 次松弛操作才能计算出A到达其他所有顶点的最短路径
二、实例
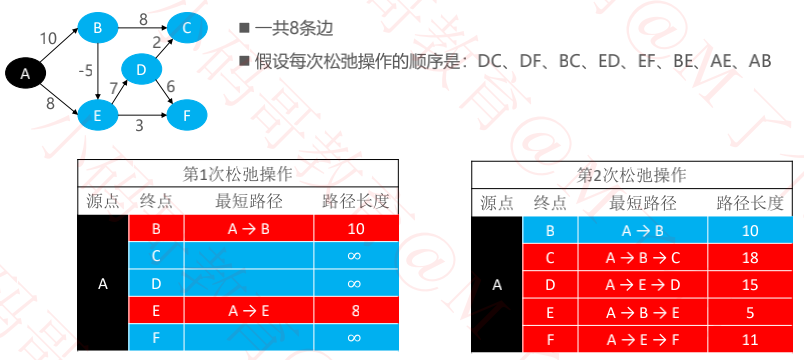
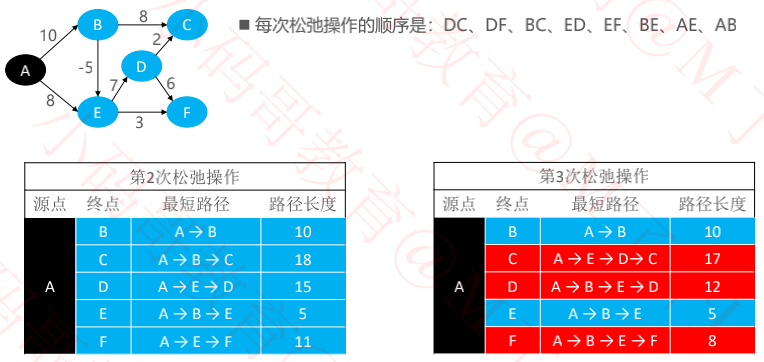
三、代码实现
/// begin到各顶点的最短路径(value:LCPathInfo)
/// @param begin 起始顶点
-(NSDictionary<id,LCPathInfo*>*)shortestPath:(id)begin{
NSDictionary * dic = [self __bellmanFord:begin];
return dic;
}
/// bellford算法返回value:LCPathInfo
/// @param begin 起始点
-(NSDictionary<id,LCPathInfo*>*)__bellmanFord:(id)begin{
LCVertex* beginVertex = [self __verticsGetKey:begin];
if (beginVertex == nil) return nil;
//value:LCPathInfo 存放已经离开桌面的顶点(起始点到vertex的权重值,已经最终确定)
NSMutableDictionary<id,LCPathInfo*> * selectedPaths = [NSMutableDictionary dictionary];
LCPathInfo* beginPathInfo = [[LCPathInfo alloc] initWithWeight:self.weightManager.zero];
[selectedPaths setObject:beginPathInfo forKey:begin];
//对每个edge进行v-1次松弛,v为顶点数量
int time = (int)self.vertics.count-1;
while (time--) {
//NSSet的输出顺序是随机的,
//但只要这个set对象不发生改变,其输出顺序永远是这个顺序
for (LCEdge* edge in self.edges) {
LCPathInfo* fromPathInfo = [selectedPaths objectForKey:edge.from.value];
if (fromPathInfo == nil) {
fromPathInfo = [[LCPathInfo alloc] init];
[selectedPaths setObject:fromPathInfo forKey:edge.from.value];
}
LCPathInfo* toPathInfo = [selectedPaths objectForKey:edge.to.value];
if (toPathInfo == nil) {
toPathInfo = [[LCPathInfo alloc] init];
[selectedPaths setObject:toPathInfo forKey:edge.to.value];
}
//对某一条边进行松弛操作
[self __relaxEdge:edge fromPathInfo:fromPathInfo toPathInfo:toPathInfo];
}
}
//再来一次验证是否有负权环
for (LCEdge* edge in self.edges) {
LCPathInfo* fromPathInfo = [selectedPaths objectForKey:edge.from.value];
if (fromPathInfo == nil) {
fromPathInfo = [[LCPathInfo alloc] init];
[selectedPaths setObject:fromPathInfo forKey:edge.from.value];
}
LCPathInfo* toPathInfo = [selectedPaths objectForKey:edge.to.value];
if (toPathInfo == nil) {
toPathInfo = [[LCPathInfo alloc] init];
[selectedPaths setObject:toPathInfo forKey:edge.to.value];
}
//对某一条边进行松弛操作
BOOL isSuccess = [self __relaxEdge:edge
fromPathInfo:fromPathInfo
toPathInfo:toPathInfo];
//
if (isSuccess) {NSLog(@"有负权环");break;}
}
//去除起始点
[selectedPaths removeObjectForKey:begin];
return selectedPaths;
}
/// 对某一条边进行松弛操作,松弛成功返回true,失败返回false
/// @param edge 边
/// @param fromPathInfo 边的起始pathInfo对象
/// @param toPathInfo 边的终止pathInfo对象
-(BOOL)__relaxEdge:(LCEdge*)edge
fromPathInfo:(LCPathInfo*)fromPathInfo
toPathInfo:(LCPathInfo*)toPathInfo{
id fromWeight = fromPathInfo.weight;
if (fromWeight == nil) return false;
id newWeight = [self.weightManager addE1:fromWeight e2:edge.weight];
//松弛操作
id toWeight = toPathInfo.weight;
if (toWeight == nil || [self.weightManager compareE1:newWeight e2:toWeight]<0) {
toPathInfo.weight = newWeight;
[toPathInfo.edgeInfos removeAllObjects];
[toPathInfo.edgeInfos addObjectsFromArray:fromPathInfo.edgeInfos];
[toPathInfo.edgeInfos addObject:edge.info];
return true;
}else{
return false;
}
}
Floyd
Floyd 属于多源最短路径算法,能够求出任意2个顶点之间的最短路径,支持负权边
时间复杂度:O(V^3),效率比执行 V 次 Dijkstra 算法要好( V 是顶点数量)
算法原理
从任意顶点 i 到任意顶点 j 的最短路径不外乎两种可能
① 直接从 i 到 j
② 从 i 经过若干个顶点到 j
假设 dist(i,j) 为顶点 i 到顶点 j 的最短路径的距离
对于每一个顶点 k,检查 dist(i,k) + dist(k,j)<dist(i,j) 是否成立
✓ 如果成立,证明从 i 到 k 再到 j 的路径比 i 直接到 j 的路径短,设置 dist(i,j) = dist(i,k) + dist(k,j)
✓ 当我们遍历完所有结点 k,dist(i,j) 中记录的便是 i 到 j 的最短路径的距离
/// 多源最短路径,返回
/// {from1Value:{toValue1:LCPathInfo
/// toValue2:LCPathInfo
/// ...
/// },
/// from2Value:{toValue1:LCPathInfo
/// toValue2:LCPathInfo
/// ...
/// },
/// ...
/// }
-(NSDictionary<id,NSDictionary<id,LCPathInfo*>*>*)shortestPath{
//初始化 {fromValue:{toValue:LCPathInfo}}
NSMutableDictionary<id,NSMutableDictionary<id,LCPathInfo*>*>* paths = [NSMutableDictionary dictionary];
for (LCEdge *edge in self.edges) {
NSMutableDictionary<id,LCPathInfo*>* map = [paths objectForKey:edge.from.value];
if (map == nil) {
map = [NSMutableDictionary dictionary];
[paths setObject:map forKey:edge.from.value];
}
LCPathInfo * pathInfo = [[LCPathInfo alloc] initWithWeight:edge.weight];
[pathInfo.edgeInfos addObject:edge.info];
[map setObject:pathInfo forKey:edge.to.value];
}
//检查 dist(v1,v2) + dist(v2,v3)<dist(v1,v3) 是否成立
__weak typeof(self) weakSelf = self;
[self.vertics enumerateKeysAndObjectsUsingBlock:^(id v2,LCVertex* vertex2, BOOL * stop) {
[weakSelf.vertics enumerateKeysAndObjectsUsingBlock:^(id v1,LCVertex* vertex1, BOOL * stop) {
[weakSelf.vertics enumerateKeysAndObjectsUsingBlock:^(id v3,LCVertex* vertex3, BOOL * stop) {
//v1、v2、v3须是三个不同的顶点
if ([v1 isEqual:v2] || [v1 isEqual:v3] || [v2 isEqual:v3]) return;
//v1->v2
LCPathInfo* pathInfo12 = [weakSelf __getPathInfoWithFromValue:v1
toValue:v2
paths:paths];
if (pathInfo12 == nil) return;
//v2->v3
LCPathInfo* pathInfo23 = [weakSelf __getPathInfoWithFromValue:v2
toValue:v3
paths:paths];
if (pathInfo23 == nil) return;
//v1->v3
LCPathInfo* pathInfo13 = [weakSelf __getPathInfoWithFromValue:v1
toValue:v3
paths:paths];
if (pathInfo13 == nil) {
pathInfo13 = [[LCPathInfo alloc] init];
[[paths objectForKey:v1] setObject:pathInfo13 forKey:v3];
}
id oldWeight = pathInfo13.weight;
id newWeight = [self.weightManager addE1:pathInfo12.weight e2:pathInfo23.weight];
if (oldWeight == nil || [self.weightManager compareE1:newWeight e2:oldWeight]<0) {
pathInfo13.weight = newWeight;
[pathInfo13.edgeInfos removeAllObjects];
[pathInfo13.edgeInfos addObjectsFromArray:pathInfo12.edgeInfos];
[pathInfo13.edgeInfos addObjectsFromArray:pathInfo23.edgeInfos];
}
}];
}];
}];
return paths;
}
/// 获取pathInfo
/// @param fromValue 起始Value
/// @param toValue 终止Value
/// @param paths NSMutableDictionary<fromValue,NSDictionary<toValue,LCPathInfo*>*>
-(LCPathInfo*)__getPathInfoWithFromValue:(id)fromValue
toValue:(id)toValue
paths:(NSMutableDictionary*)paths{
NSDictionary * map = paths[fromValue];
return map == nil?nil:map[toValue];
}
行者常至,为者常成!
