目录
最短路径(Shortest Path)
一、有权图
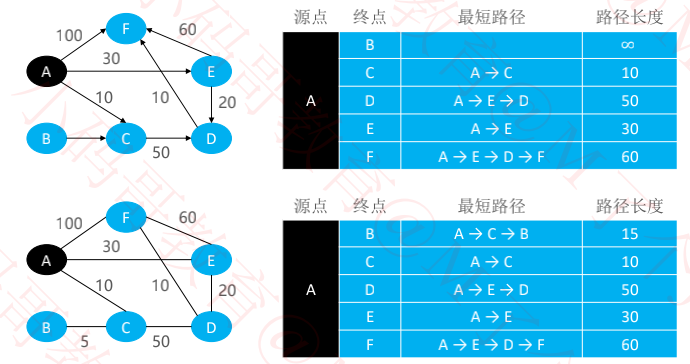
最短路径是指两顶点之间权值之和最小的路径(有向图、无向图均适用,不能有负权环)
二、无权图
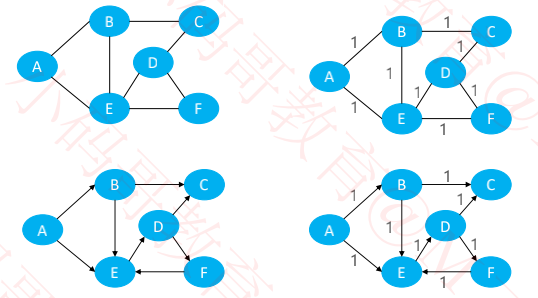
无权图相当于是全部边权值为1的有权图
三、负权边
有负权边,但没有负权环时,存在最短路径
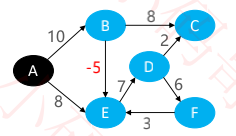
A到E的最短路径是:A → B → E
四、负权环
有负权环时,不存在最短路径
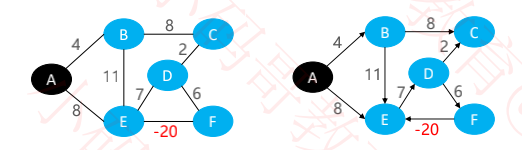
通过负权环, A到E的路径可以无限短
A → E → D → F → E → D → F →E → D → F →E → D → F → E → ……
五、最短路径
最短路径的典型应用之一:路径规划问题
求解最短路径的3个经典算法
单源最短路径算法
✓ Dijkstra(迪杰斯特拉算法)
✓ Bellman-Ford(贝尔曼-福特算法)
多源最短路径算法
✓ Floyd(弗洛伊德算法)
Dijkstra(迪杰斯特拉算法)
一、Dijkstra
属于单源最短路径算法,用于计算一个顶点到其他所有顶点的最短路径
使用前提:不能有负权边
时间复杂度:可优化至 O(ElogV) ,E 是边数量,V 是节点数量
由荷兰的科学家 Edsger Wybe Dijkstra 发明,曾在1972年获得图灵奖

二、等价思考
Dijkstra 的原理其实跟生活中的一些自然现象完全一样
把每1个顶点想象成是1块小石头
每1条边想象成是1条绳子,每一条绳子都连接着2块小石头,边的权值就是绳子的长度
将小石头和绳子平放在一张桌子上(下图是一张俯视图,图中黄颜色的是桌子)
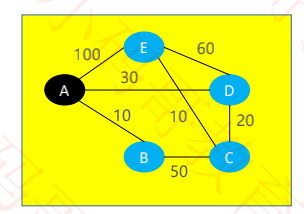
接下来想象一下,手拽着小石头A,慢慢地向上提起来,远离桌面
B、D、C、E会依次离开桌面
最后绷直的绳子就是A到其他小石头的最短路径
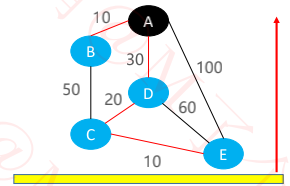
有一个很关键的信息
后离开桌面的小石头,都是被先离开桌面的小石头拉起来的
三、执行过程
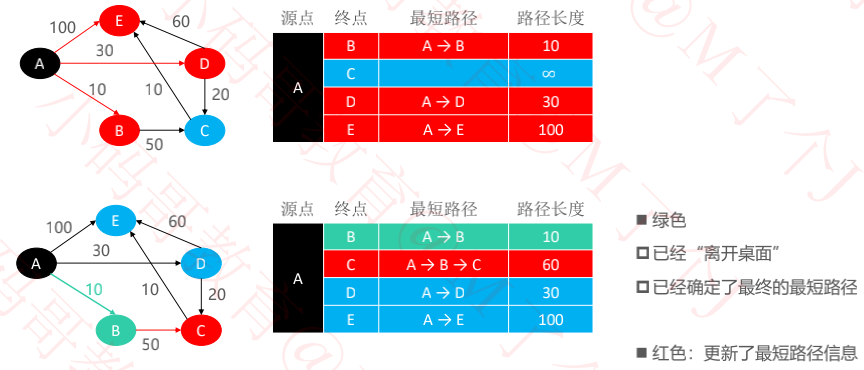
松弛操作(Relaxation):更新2个顶点之间的最短路径
这里一般是指:更新源点到另一个点的最短路径
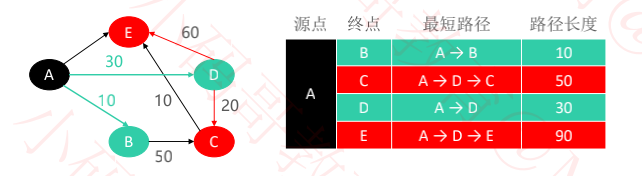
松弛操作的意义:尝试找出更短的最短路径
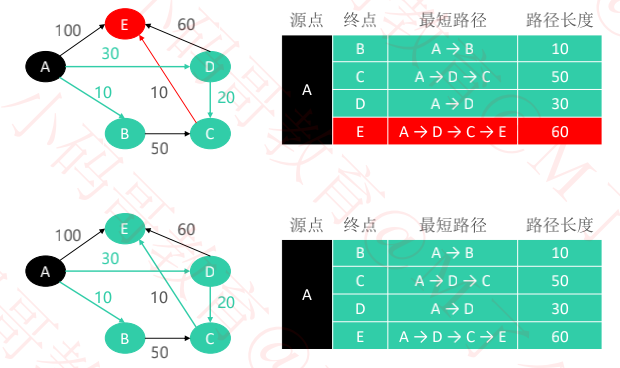
确定A到D的最短路径后,对DC、DE边进行松弛操作,更新了A到C、A到E的最短路径
四、代码实现
/// begin到各顶点的最短路径(value:LCPathInfo)
/// @param begin 起始顶点
-(NSDictionary<id,LCPathInfo*>*)shortestPath:(id)begin{
NSDictionary * dic = [self __dijkstra:begin];
return dic;
}
/// dijkstra算法返回value:LCPathInfo
/// @param begin 起始点
-(NSDictionary<id,LCPathInfo*>*)__dijkstra:(id)begin{
LCVertex* beginVertex = [self __verticsGetKey:begin];
if (beginVertex == nil) return nil;
//value:LCPathInfo 存放已经离开桌面的顶点(起始点到vertex的权重值,已经最终确定)
NSMutableDictionary<id,LCPathInfo*> * selectedPaths = [NSMutableDictionary dictionary];
//vertex:LCPathInfo 存放可能离开桌面的顶点(起始点到vertex的权重值,还未最终确定)
NSMutableDictionary<LCVertex*,LCPathInfo*> * paths = [NSMutableDictionary dictionary];
//初始化paths
[paths setObject:[[LCPathInfo alloc] initWithWeight:self.weightManager.zero]
forKey:beginVertex];
while (paths.count) {
//从可能离开的顶点中,找到将要离开桌面的顶点
pair<LCVertex*, LCPathInfo*> minEntry = [self __getMinPath:paths];
//离开桌面
LCVertex* minVertex = minEntry.first; //vertex
LCPathInfo* minPathInfo = minEntry.second; //pathInfo
id minValue = minVertex.value; //value
//value:pathInfo 放入已选
[selectedPaths setObject:minPathInfo forKey:minValue];
NSLog(@"selectedPaths = %@",selectedPaths);
//vertex:pathInfo 从待选中移除
[paths removeObjectForKey:minVertex];
// 对minVertex的outEdges进行松弛操作
for (LCEdge* edge in minVertex.outEdges) {
//如果已经被选择,不再重复进行选择
if ([selectedPaths.allKeys containsObject:edge.to.value]) continue;
LCPathInfo * fromPathInfo = minPathInfo;
LCPathInfo * toPathInfo = [paths objectForKey:edge.to];
if (toPathInfo == nil) {
toPathInfo = [[LCPathInfo alloc] init];
[paths setObject:toPathInfo forKey:edge.to];
}
//对某一条进行松弛操作
[self __relaxEdge:edge fromPathInfo:fromPathInfo toPathInfo:toPathInfo];
}
}
//去除起始点
[selectedPaths removeObjectForKey:begin];
return selectedPaths;
}
/// 从NSDictionary<LCVertex*,LCPathInfo*>*获取最小权重的pair<LCVertex*, LCPathInfo*>返回
/// @param paths NSDictionary<LCVertex*,LCPathInfo*>*
-(pair<LCVertex*, LCPathInfo*>)__getMinPath:(NSDictionary<LCVertex*,LCPathInfo*>*)paths{
__block LCVertex * minVertex;
__block LCPathInfo * minPathInfo;
//vertex:weight
[paths enumerateKeysAndObjectsUsingBlock:^(LCVertex* key, LCPathInfo* pathInfo, BOOL * stop) {
if (minPathInfo == nil || [self.weightManager compareE1:pathInfo.weight e2:minPathInfo.weight]<0) {
minPathInfo = pathInfo;
minVertex = key;
}
}];
return pair<LCVertex*, id>(minVertex,minPathInfo);
}
/// 对某一条边进行松弛操作,松弛成功返回true,失败返回false
/// @param edge 边
/// @param fromPathInfo 边的起始pathInfo对象
/// @param toPathInfo 边的终止pathInfo对象
-(BOOL)__relaxEdge:(LCEdge*)edge
fromPathInfo:(LCPathInfo*)fromPathInfo
toPathInfo:(LCPathInfo*)toPathInfo{
id fromWeight = fromPathInfo.weight;
if (fromWeight == nil) return false;
id newWeight = [self.weightManager addE1:fromWeight e2:edge.weight];
//松弛操作
id toWeight = toPathInfo.weight;
if (toWeight == nil || [self.weightManager compareE1:newWeight e2:toWeight]<0) {
toPathInfo.weight = newWeight;
[toPathInfo.edgeInfos removeAllObjects];
[toPathInfo.edgeInfos addObjectsFromArray:fromPathInfo.edgeInfos];
[toPathInfo.edgeInfos addObject:edge.info];
return true;
}else{
return false;
}
}
行者常至,为者常成!
