目录
生成树(Spanning Tree)
一、生成树(Spanning Tree),也称为支撑树
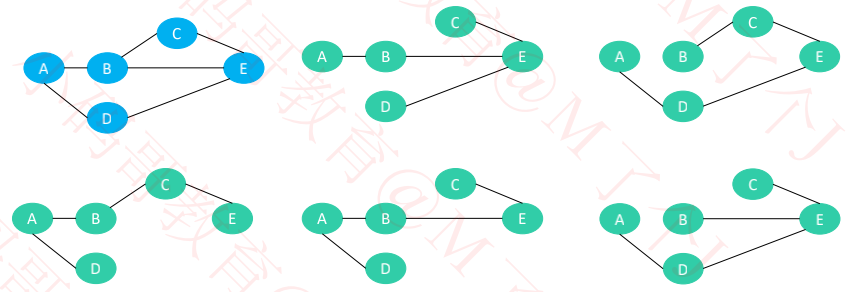
连通图的极小连通子图,它含有图中全部的 n 个顶点,恰好只有 n – 1 条边
二、最小生成树(Minimum Spanning Tree)
最小生成树(Minimum Spanning Tree,简称MST)
也称为最小权重生成树(Minimum Weight Spanning Tree)、最小支撑树
是所有生成树中,总权值最小的那棵
适用于有权的连通图(无向)
最小生成树在许多领域都有重要的作用,例如
要在 n 个城市之间铺设光缆,使它们都可以通信,铺设光缆的费用很高,且各个城市之间因为距离不同等因素,铺设光缆的费用也不同如何使铺设光缆的总费用最低?
如果图的每一条边的权值都互不相同,那么最小生成树将只有一个,否则可能会有多个最小生成树
求最小生成树的2个经典算法
Prim(普里姆算法)
Kruskal(克鲁斯克尔算法)
切分定理
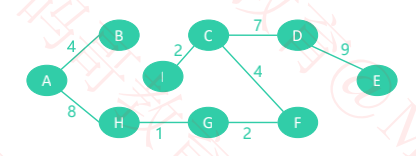
切分(Cut):把图中的节点分为两部分,称为一个切分
下图有个切分 C = (S, T),S = {A, B, D},T = {C, E}

横切边(Crossing Edge):如果一个边的两个顶点,分别属于切分的两部分,这个边称为横切边
比如上图的边 BC、BE、DE 就是横切边
切分定理:给定任意切分,横切边中权值最小的边必然属于最小生成树
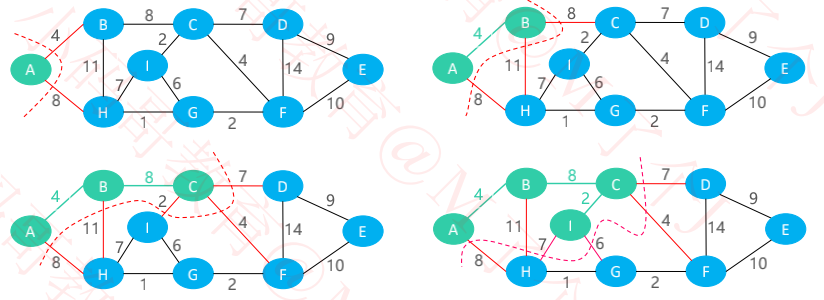
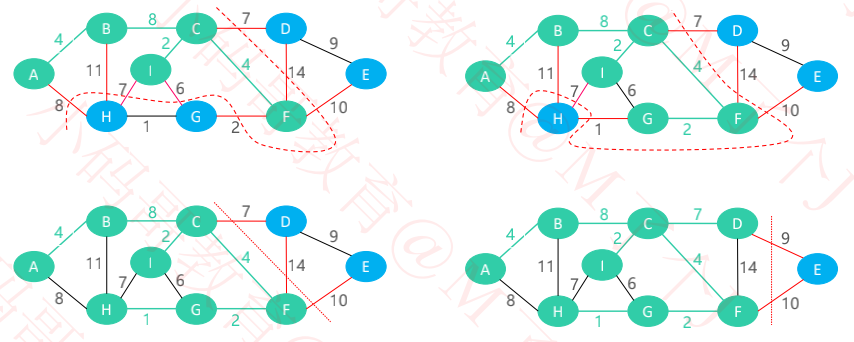
Prim算法
一、原理
假设 G = (V,E) 是有权的连通图(无向),A 是 G 中最小生成树的边集
算法从 S = { u0 }(u0 ∈ V),A = { } 开始,重复执行下述操作,直到 S = V 为止
找到切分 C = (S,V – S) 的最小横切边 (u0,v0) 并入集合 A,同时将 v0 并入集合 S
二、执行流程

三、代码实现
//prim 算法
-(NSSet<LCEdgeInfo*>*)__prim{
//从一个vertex开始
NSEnumerator * itrator = self.vertics.allValues.objectEnumerator;
LCVertex* vertex = itrator.nextObject;
if (vertex == nil) return nil;
//最终返回的边集合
NSMutableSet * edgeInfos = [NSMutableSet set];
//已经分离出的vertex
NSMutableSet * addedVertices = [NSMutableSet set];
[addedVertices addObject:vertex];
//outEdges 创建小顶堆 按边的权重进行比较
LCBinaryHeap * heap = [LCBinaryHeap binaryHeapWithSet:vertex.outEdges
comparator:self.edgeComparator];
//所有顶点的数量
int verticesSize = (int)self.vertics.allKeys.count;
while (!heap.isEmpty && addedVertices.count < verticesSize) {
LCEdge* edge = heap.remove;
//如果edge.to包含在addedVertices 证明这条路已经被选过了
if ([addedVertices containsObject:edge.to]) continue;
//添加最小权重边
[edgeInfos addObject:edge.info];
//添加分离出的顶点
[addedVertices addObject:edge.to];
//添加分离出顶点的所有outedge,为下次切分做准备
[heap addAllWithSet:edge.to.outEdges];
}
return [edgeInfos copy];
}
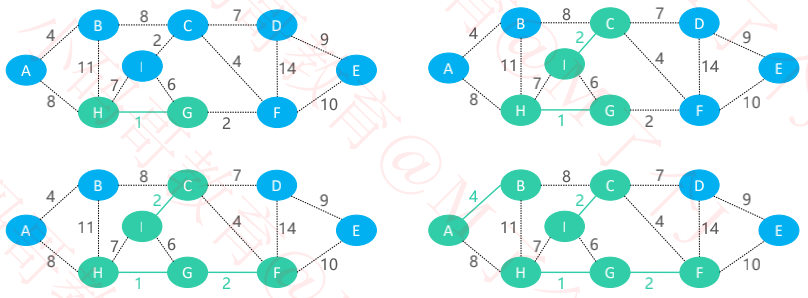
Kruskal算法
一、原理
按照边的权重顺序(从小到大)将边加入生成树中,直到生成树中含有 V – 1 条边为止( V 是顶点数量)
若加入该边会与生成树形成环,则不加入该边
二、执行流程
从第3条边开始,可能会与生成树形成环
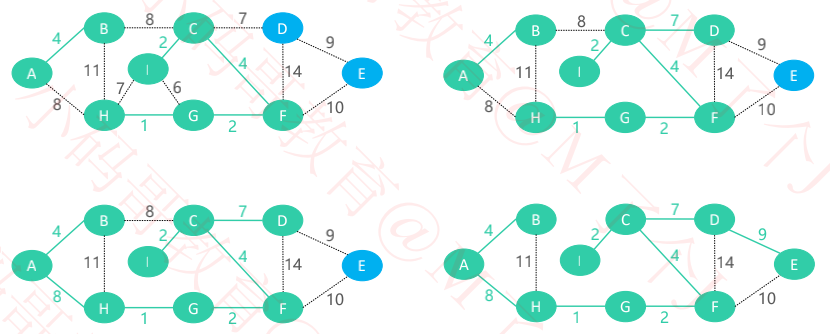
三、代码实现
//kruskal算法
-(NSSet<LCEdgeInfo*>*)__kruskal{
int edgeSize = (int)self.vertics.count-1;
if (edgeSize == -1) return nil;
//最终返回的边集合
NSMutableSet * edgeInfos = [NSMutableSet set];
//Edges 创建小顶堆 按边的权重进行比较
LCBinaryHeap * heap = [LCBinaryHeap binaryHeapWithSet:self.edges
comparator:self.edgeComparator];
//并查集,用于判断加入边是否会形成环
LCGenericUnionFind * unionFind = [[LCGenericUnionFind alloc] init];
[self.vertics enumerateKeysAndObjectsUsingBlock:^(id key, LCVertex* vertex, BOOL* stop) {
[unionFind makeSet:vertex];
}];
while (!heap.isEmpty && edgeInfos.count < edgeSize) {
LCEdge * edge = [heap remove];
//如果from 跟 to 在 同一个集合 那么合并后就会形成环
if([unionFind isSameWithV1:edge.from v2:edge.to]) continue;
[edgeInfos addObject:edge];
[unionFind unionWithV1:edge.from v2:edge.to];
}
return [edgeInfos copy];
}
行者常至,为者常成!
