【进阶】9、图（三）

2014-03-09 | 阅读：

遍历

图的遍历

从图中某一顶点出发访问图中其余顶点，且每一个顶点仅被访问一次

图有2种常见的遍历方式（有向图、无向图都适用）

广度优先搜索（Breadth First Search，BFS），又称为宽度优先搜索、横向优先搜索

深度优先搜索（Depth First Search，DFS）

发明“深度优先搜索”算法的2位科学家在1986年共同获得计算机领域的最高奖：图灵奖

广度优先搜索BFS（Breadth First Search）

一、之前所学的二叉树层序遍历就是一种广度优先搜索

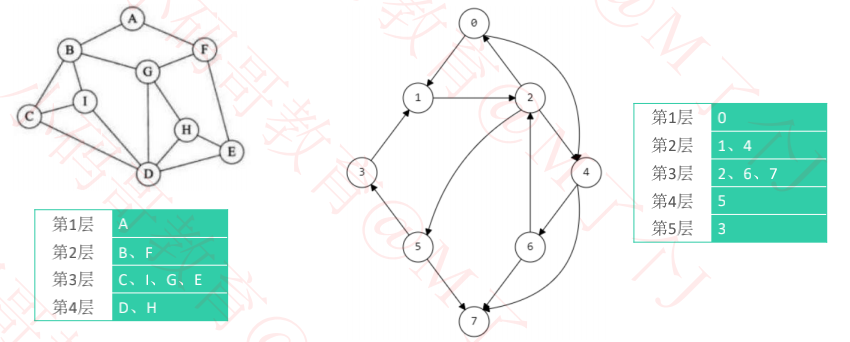
二、分层

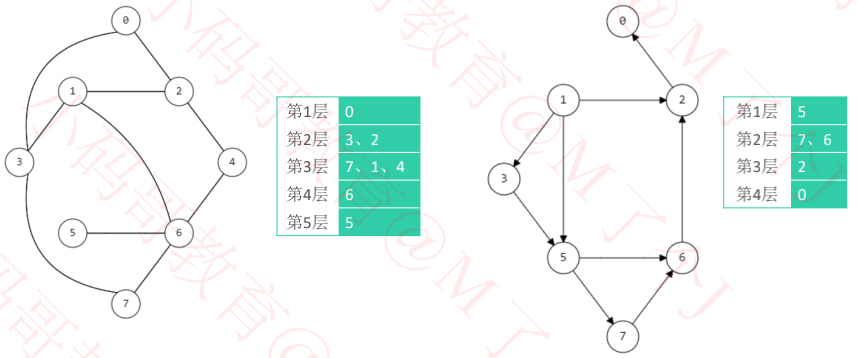
与某点直接相连的点，位于该点的下一层。

广度优先搜索，因为起始点的不同，遍历结果有所不同。同时也不能保证将每一个点都遍历到

三、广度优先搜索思路

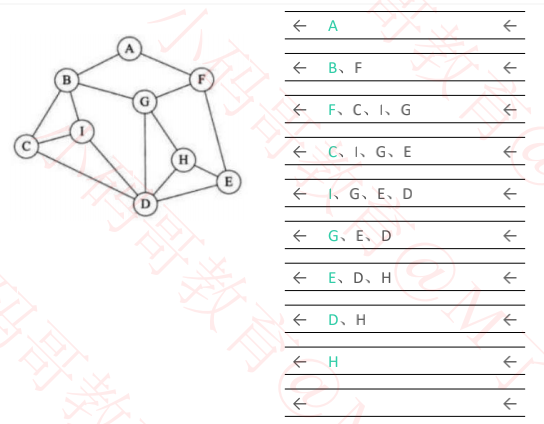
四、广度优先搜索-实现

/// 宽度优先搜索
/// @param begin 起始顶点
/// @param vistor 访问器
-(void)bfs:(id)begin Vistor:(Vistor)vistor{

    if (!vistor) return;
    LCVertex* beginVertex = [self __verticsGetKey:begin];
    if (beginVertex == nil) return;
    
    BOOL stop = false;
    
    //存放已经访问过的顶点，避免重复访问
    NSMutableSet * visitedVertics = [NSMutableSet set];
    
    queue<LCVertex*>* vertexQueue = new queue<LCVertex*>();
    vertexQueue->push(beginVertex);
    while (vertexQueue->size()) {
        
        LCVertex* vertex = vertexQueue->front();
        vertexQueue->pop();
        vistor(vertex.value,&stop);
        if (stop) return;
        
        [vertex.outEdges enumerateObjectsUsingBlock:^(LCEdge*  _Nonnull obj, BOOL * _Nonnull stop) {
            
            if(![visitedVertics containsObject:obj.to]){
                vertexQueue->push(obj.to);
                [visitedVertics addObject:obj.to];
            }
        }];
    }
    
    delete vertexQueue;
}

深度优先搜索DFS（Depth First Search）

一、之前所学的二叉树前序遍历就是一种深度优先搜索

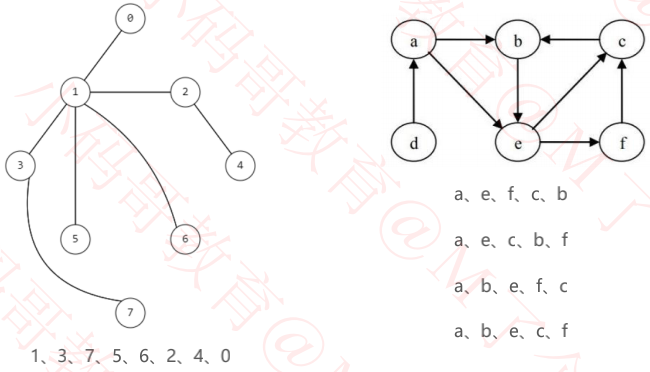
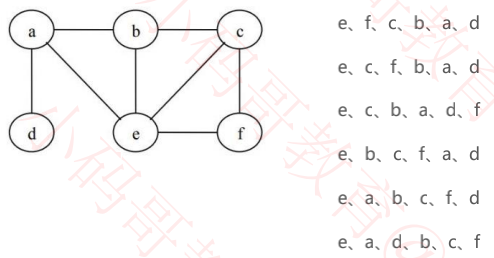
二、深度优先搜索递归实现

/// 深度优先搜索
/// @param begin 起始顶点
/// @param vistor 访问器
-(void)dfs2:(id)begin Vistor:(Vistor)vistor{
    if (!vistor) return;
    LCVertex* beginVertex = [self __verticsGetKey:begin];
    if (beginVertex == nil) return;
    
    BOOL stop = false;
    
    [self __dfs:beginVertex
visitedVertices:[NSMutableSet set]
         Vistor:(Vistor)vistor
           stop:&stop];
}


-(void)__dfs:(LCVertex*)beginVertex
visitedVertices:(NSMutableSet*)visitedVertices
      Vistor:(Vistor)vistor
        stop:(BOOL*)stop{
    
    [visitedVertices addObject:beginVertex];
    
    vistor(beginVertex.value,stop);
    if(*stop) return;
    
    
    [beginVertex.outEdges enumerateObjectsUsingBlock:^(LCEdge* edge, BOOL * _Nonnull stop) {
        if (![visitedVertices containsObject:edge.to]) {
            
            [self __dfs:edge.to
        visitedVertices:visitedVertices
                 Vistor:(Vistor)vistor
                   stop:stop];
        }
    }];
}

三、深度优先搜索非递归实现

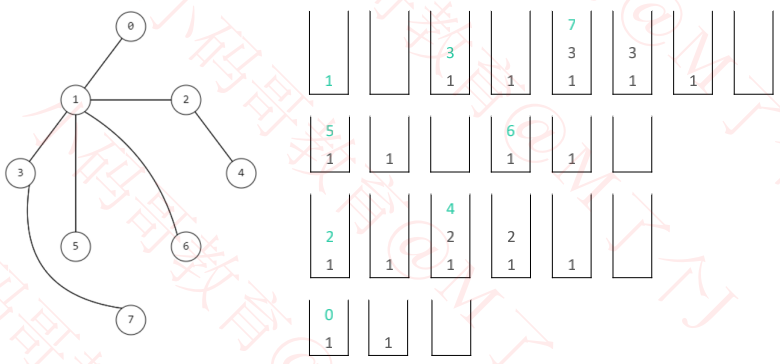
/// 深度优先搜索
/// @param begin 起始顶点
/// @param vistor 访问器
-(void)dfs:(id)begin Vistor:(Vistor)vistor{
    if (!vistor) return;
    LCVertex* beginVertex = [self __verticsGetKey:begin];
    if (beginVertex == nil) return;
    
    __block BOOL outstop = false;

    //存放已经访问过的顶点，避免重复访问
    NSMutableSet * visitedVertics = [NSMutableSet set];
    stack<LCVertex*>* vertexStack = new stack<LCVertex*>();
    
    vertexStack->push(beginVertex);
    [visitedVertics addObject:beginVertex];

    vistor(beginVertex.value,&outstop);
    if (outstop) return;

    while (vertexStack->size()) {
        
        LCVertex* vertex = vertexStack->top();
        vertexStack->pop();
        
        
        for (LCEdge*edge in vertex.outEdges) {
            
            //如果已经遍历过，不再处理
            if ([visitedVertics containsObject:edge.to]) continue;

            vertexStack->push(edge.from);
            vertexStack->push(edge.to);
            [visitedVertics addObject:edge.to];
            
            vistor(edge.to.value,&outstop);
            if (outstop) return;
            
            break;
        }
    }
    
    delete vertexStack;

}

AOV网（Activity On Vertex Network）

一项大的工程常被分为多个小的子工程

子工程之间可能存在一定的先后顺序，即某些子工程必须在其他的一些子工程完成后才能开始

在现代化管理中，人们常用有向图来描述和分析一项工程的计划和实施过程，子工程被称为活动（Activity）

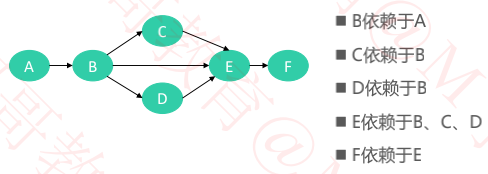
以顶点表示活动、有向边表示活动之间的先后关系，这样的图简称为 AOV 网

标准的AOV网必须是一个有向无环图（Directed Acyclic Graph，简称 DAG）

拓扑排序（Topological Sort）

一、拓扑排序介绍

前驱活动：有向边起点的活动称为终点的前驱活动,只有当一个活动的前驱全部都完成后，这个活动才能进行

后继活动：有向边终点的活动称为起点的后继活动

什么是拓扑排序？

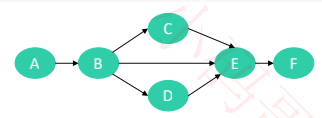
将 AOV 网中所有活动排成一个序列，使得每个活动的前驱活动都排在该活动的前面

比如上图的拓扑排序结果是：A、B、C、D、E、F 或者 A、B、D、C、E、F （结果并不一定是唯一的）

二、拓扑排序思路

可以使用卡恩算法（Kahn于1962年提出）完成拓扑排序

假设 L 是存放拓扑排序结果的列表

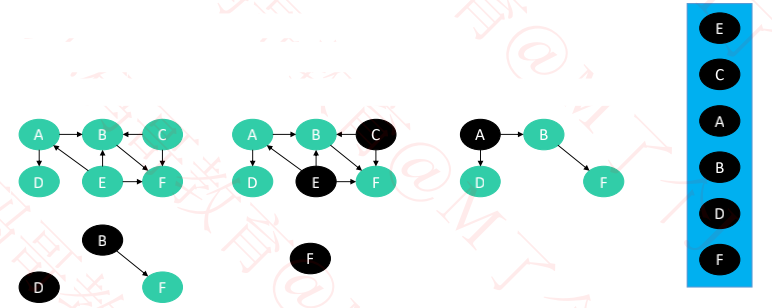
① 把所有入度为 0 的顶点放入 L 中，然后把这些顶点从图中去掉

② 重复操作 ①，直到找不到入度为 0 的顶点
如果此时 L 中的元素个数和顶点总数相同，说明拓扑排序完成
如果此时 L 中的元素个数少于顶点总数，说明原图中存在环，无法进行拓扑排序

三、拓扑排序实现

/// 拓扑排序
-(NSArray*)topologicalSort{
    
    //存放最终的排序结果
    NSMutableArray* sortArray = [NSMutableArray array];
    
    //存放入度为0的顶点
    queue<LCVertex*>* vertexQueue = new queue<LCVertex*>();
    
    //存放顶点实时的入度值
    map<LCVertex*,int>* inSizes = new map<LCVertex*, int>();

    //初始化（将度为0的节点都放入队列）
    [self.vertics enumerateKeysAndObjectsUsingBlock:^(NSString* key,LCVertex* vertex,BOOL*stop){
        int inSize = (int)vertex.inEdges.count;
        if (inSize == 0) {
            vertexQueue->push(vertex);
        }else{
            inSizes->insert(pair<LCVertex*, int>(vertex, inSize));
        }
    }];
    
    
    while (vertexQueue->size()) {
        LCVertex* frontVertex = vertexQueue->front();
        vertexQueue->pop();
        
        //放入返回结果中
        [sortArray addObject:frontVertex.value];
        
        //通过入度值的变化来模拟删除
        for (LCEdge*edge in frontVertex.outEdges) {
            
            auto it = inSizes->find(edge.to);
            int newSize = it->second-1;
            
            if (newSize == 0) {
                vertexQueue->push(edge.to);
            }else{
                //更改map的value
                it->second = newSize;
            }
        }
    }
    
    delete vertexQueue;
    delete inSizes;
    return [sortArray copy];
}

行者常至，为者常成！

JHHK