目录
动态规划(Dynamic Programming)
一、常规步骤
动态规划中的“动态”可以理解为是“会变化的状态”
① 定义状态(状态是原问题、子问题的解)
✓ 比如定义 dp(i) 的含义
② 设置初始状态(边界)
✓ 比如设置 dp(0) 的值
③ 确定状态转移方程
✓ 比如确定 dp(i) 和 dp(i – 1) 的关系
二、动态规划的一些相关概念
来自维基百科的解释
Dynamic Programming is a method for solving a complex problem by breaking it down into a
collection of simpler subproblems, solving each of those subproblems just once, and storing their
solutions.
① 将复杂的原问题拆解成若干个简单的子问题
② 每个子问题仅仅解决1次,并保存它们的解
③ 最后推导出原问题的解
可以用动态规划来解决的问题,通常具备2个特点
1、最优子结构(最优化原理):通过求解子问题的最优解,可以获得原问题的最优解
2、无后效性
✓ 某阶段的状态一旦确定,则此后过程的演变不再受此前各状态及决策的影响(未来与过去无关)
✓ 在推导后面阶段的状态时,只关心前面阶段的具体状态值,不关心这个状态是怎么一步步推导出来的
三、后效性
1、无后效性
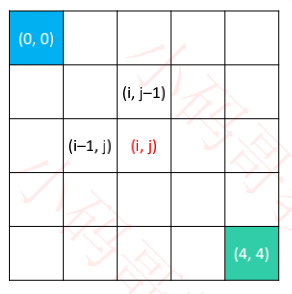
从起点(0, 0)走到终点(4, 4)一共有多少种走法?只能向右、向下走
假设 dp(i, j) 是从(0, 0)走到(i, j)的走法
dp(i, 0) = dp(0, j) = 1
dp(i, j) = dp(i, j – 1) + dp(i – 1, j)
推导 dp(i, j) 时只需要用到 dp(i, j – 1)、dp(i – 1, j) 的值
不需要关心 dp(i, j – 1)、dp(i – 1, j) 的值是怎么求出来的
2、有后效性
如果可以向左、向右、向上、向下走,并且同一个格子不能走 2 次
dp(i, j) 下一步要怎么走,还要关心上一步是怎么来的
也就是还要关心 dp(i, j – 1)、dp(i – 1, j) 是怎么来的?
最大连续子序列和
一、分析
给定一个长度为 n 的整数序列,求它的最大连续子序列和
比如 –2、1、–3、4、–1、2、1、–5、4 的最大连续子序列和是 4 + (–1) + 2 + 1 = 6
状态定义
假设 dp(i) 是以 nums[i] 结尾的最大连续子序列和(nums是整个序列)
✓ 以 nums[0] –2 结尾的最大连续子序列是 –2,所以 dp(0) = –2
✓ 以 nums[1] 1 结尾的最大连续子序列是 1,所以 dp(1) = 1
✓ 以 nums[2] –3 结尾的最大连续子序列是 1、–3,所以 dp(2) = dp(1) + (–3) = –2
✓ 以 nums[3] 4 结尾的最大连续子序列是 4,所以 dp(3) = 4
✓ 以 nums[4] –1 结尾的最大连续子序列是 4、–1,所以 dp(4) = dp(3) + (–1) = 3
✓ 以 nums[5] 2 结尾的最大连续子序列是 4、–1、2,所以 dp(5) = dp(4) + 2 = 5
✓ 以 nums[6] 1 结尾的最大连续子序列是 4、–1、2、1,所以 dp(6) = dp(5) + 1 = 6
✓ 以 nums[7] –5 结尾的最大连续子序列是 4、–1、2、1、–5,所以 dp(7) = dp(6) + (–5) = 1
✓ 以 nums[8] 4 结尾的最大连续子序列是 4、–1、2、1、–5、4,所以 dp(8) = dp(7) + 4 = 5
二、状态转移方程
状态转移方程
如果 dp(i – 1) ≤ 0,那么 dp(i) = nums[i]
如果 dp(i – 1) > 0,那么 dp(i) = dp(i – 1) + nums[i]
初始状态
dp(0) 的值是 nums[0]
最终的解
最大连续子序列和是所有 dp(i) 中的最大值 max { dp(i) },i ∈ [0, nums.length)
三、代码实现
+(int)maxSubArray:(NSArray*)nums{
if (nums == nil || nums.count == 0) return INT_MIN;
NSMutableArray * dp = [NSMutableArray array];
//初始化dp[0]
dp[0] = nums[0];
//最大值默认 dp[0]
int max = [dp[0] intValue];
for (int i = 1; i<nums.count; i++) {
int prev = [dp[i-1] intValue];
if (prev > 0) {
dp[i] = @(prev + [nums[i] intValue]);
}else{
dp[i] = nums[i];
}
max = MAX(max, [dp[i] intValue]);
}
return max ;
}
空间复杂度:O(n),时间复杂度:O(n)
四、代码优化
//优化减少不必要的空间开销
+(int)maxSubArray2:(NSArray*)nums{
if (nums == nil || nums.count == 0) return INT_MIN;
//初始化dp
int dp = [nums[0] intValue];
//最大值默认 nums[0]
int max = dp;
for (int i = 1; i<nums.count; i++) {
if (dp > 0) {
dp = dp + [nums[i] intValue];
}else{
dp = [nums[i] intValue];
}
max = MAX(max, dp);
}
return max ;
}
空间复杂度:O(1),时间复杂度:O(n)
最长上升子序列(LIS)
一、分析
最长上升子序列(最长递增子序列,Longest Increasing Subsequence,LIS)
给定一个无序的整数序列,求出它最长上升子序列的长度(要求严格上升)
比如 [10, 2, 2, 5, 1, 7, 101, 18] 的最长上升子序列是 [2, 5, 7, 101]、[2, 5, 7, 18],长度是 4
假设数组是 nums, [10, 2, 2, 5, 1, 7, 101, 18]
dp(i) 是以 nums[i] 结尾的最长上升子序列的长度,i ∈ [0, nums.length)
✓ 以 nums[0] 10 结尾的最长上升子序列是 10,所以 dp(0) = 1
✓ 以 nums[1] 2 结尾的最长上升子序列是 2,所以 dp(1) = 1
✓ 以 nums[2] 2 结尾的最长上升子序列是 2,所以 dp(2) = 1
✓ 以 nums[3] 5 结尾的最长上升子序列是 2、5,所以 dp(3) = dp(1) + 1 = dp(2) + 1 = 2
✓ 以 nums[4] 1 结尾的最长上升子序列是 1,所以 dp(4) = 1
✓ 以 nums[5] 7 结尾的最长上升子序列是 2、5、7,所以 dp(5) = dp(3) + 1 = 3
✓ 以 nums[6] 101 结尾的最长上升子序列是 2、5、7、101,所以 dp(6) = dp(5) + 1 = 4
✓ 以 nums[7] 18 结尾的最长上升子序列是 2、5、7、18,所以 dp(7) = dp(5) + 1 = 4
最长上升子序列的长度是所有 dp(i) 中的最大值 max { dp(i) },i ∈ [0, nums.length)
二、状态转移方程
遍历 j ∈ [0, i)
当 nums[i] > nums[j]
✓ nums[i] 可以接在 nums[j] 后面,形成一个比 dp(j) 更长的上升子序列,长度为 dp(j) + 1
✓ dp(i) = max { dp(i), dp(j) + 1 }
当 nums[i] ≤ nums[j]
✓ nums[i] 不能接在 nums[j] 后面,跳过此次遍历(continue)
状态的初始值
dp(0) = 1
所有的 dp(i) 默认都初始化为 1
三、代码实现
+(int)lengthOfLIS:(NSArray*)nums{
if (nums == nil || nums.count == 0) return 0;
//dp(i) 是以 nums[i] 结尾的最长上升子序列的长度,i ∈ [0, nums.length)
NSMutableArray * dp = [NSMutableArray array];
int maxLength = 1; //最大长度 默认1
dp[0] = @(1); //初始化dp[0]
//
for (int i = 1; i<nums.count; i++) {
//初始化dp[i]为1
dp[i] = @(1);
for (int j = 0; j < i; j++) {
//上升
if ([nums[j] intValue] >= [nums[i] intValue]) continue;
//更新dp[i]
dp[i] = @(MAX([dp[i] intValue],[dp[j] intValue] + 1));
}
//更新最大值
maxLength = MAX(maxLength, [dp[i] intValue]);
}
return maxLength;
}
空间复杂度:O(n),时间复杂度:O(n^2)
最长上升子序列-二分搜索实现
10 2 2 5 1 7 101 18
把每个数字看做是一张扑克牌,从左到右按顺序处理每一个扑克牌
将它压在(从左边数过来)第一个牌顶 ≥ 它的牌堆上面
如果找不到牌顶 ≥ 它的牌堆,就在最右边新建一个牌堆,将它放入这个新牌堆中
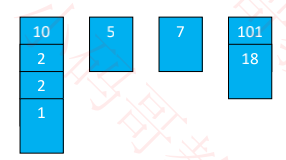
当处理完所有牌,最终牌堆的数量就是最长上升子序列的长度
代码实现
+(int)lengthOfLIS2:(NSArray*)nums{
if (nums == nil || nums.count == 0) return 0;
//存放每一堆扑克牌的顶部元素
NSMutableArray<NSNumber*> * top = [NSMutableArray array];
//初始最大长度为0
int len = 0;
for (NSNumber * num in nums) {
//二分搜索寻找插入位置
int begin = 0,end = len;
while (begin < end) {
int mid = (begin + end) >> 1;
if (num.intValue <= top[mid].intValue) {
end = mid;
}else{
begin = mid+1;
}
}
//更新或新建一堆扑克牌
top[begin] = num;
//插入位置等于len,新建了一个堆
if (begin == len) len++;
}
return len;
}
空间复杂度:O(n)
时间复杂度:O (nlogn)
行者常至,为者常成!
