目录
最长公共子序列(Longest Common Subsequence,LCS)
一、问题
求两个序列的最长公共子序列长度
[1, 3, 5, 9, 10]
和
[1, 4, 9, 10]
的最长公共子序列是 [1, 9, 10],长度为 3
ABCBDAB 和 BDCABA 的最长公共子序列长度是 4,可能是
✓ ABCBDAB
和
BDCABA > BDAB
✓ ABCBDAB
和
BDCABA > BDAB
✓ ABCBDAB 和 BDCABA > BCAB
✓ ABCBDAB 和 BDCABA > BCBA
二、思路

代码实现
一、递归实现
+(int)lcsnums1:(NSArray*)nums1 nums2:(NSArray*)nums2{
if (nums1 == nil || nums1.count == 0) return 0;
if (nums2 == nil || nums2.count == 0) return 0;
return [self __lcsnums1:nums1
n1:(int)nums1.count
nums2:nums2
n2:(int)nums2.count];
}
/// 返回最长公共子序列的长度
/// @param nums1 序列1
/// @param n1 序列1长度
/// @param nums2 序列2
/// @param n2 序列2长度
+(int)__lcsnums1:(NSArray*)nums1 n1:(int)n1 nums2:(NSArray*)nums2 n2:(int)n2{
//递归基
if (n1 == 0 || n2 == 0) return 0;
if ([nums1[n1-1] intValue] == [nums2[n2-1] intValue]){
return [self __lcsnums1:nums1 n1:n1-1 nums2:nums2 n2:n2-1]+1;
}else{
int length1 = [self __lcsnums1:nums1 n1:n1 nums2:nums2 n2:n2-1];
int length2 = [self __lcsnums1:nums1 n1:n1-1 nums2:nums2 n2:n2];
return MAX(length1, length2);
}
}
空间复杂度:O(k) , k = min{n, m},n、m 是 2 个序列的长度
时间复杂度:O(2^n) ,当 n = m 时
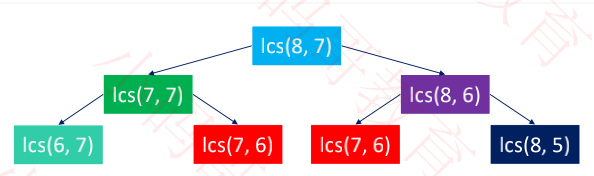
出现了重复的递归调用
二、非递归实现
+(int)lcs2nums1:(NSArray*)nums1 nums2:(NSArray*)nums2{
if (nums1 == nil || nums1.count == 0) return 0;
if (nums2 == nil || nums2.count == 0) return 0;
//dp[i][j]:num1[i-1] 和 num2[j-1] 最长公共子序列的长度
NSMutableArray<NSMutableArray*> * dp = [NSMutableArray array];
for (int row = 0; row<=nums1.count; row++) {
dp[row] = [NSMutableArray array];
for (int col = 0; col <= nums2.count; col++) {
dp[row][col] = @(0);
}
}
for (int row = 1; row <= nums1.count; row++) {
for (int col = 1; col <= nums2.count; col++) {
//状态转移方程
if ([nums1[row-1] intValue] == [nums2[col-1] intValue]) {
dp[row][col] = @([dp[row-1][col-1] intValue] + 1);
}else{
int length1 = [dp[row][col-1] intValue];
int length2 = [dp[row-1][col] intValue];
dp[row][col] = @(MAX(length1, length2));
}
}
}
return [dp[nums1.count][nums2.count] intValue];
}
空间复杂度:O(n ∗ m)
时间复杂度:O(n ∗ m)
dp 数组的计算结果如下所示
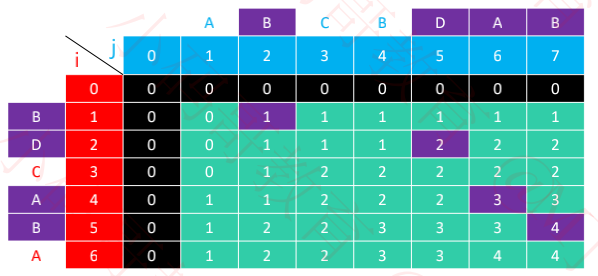
三、非递归实现(滚动数组)
可以使用滚动数组优化空间复杂度
+(int)lcs3nums1:(NSArray*)nums1 nums2:(NSArray*)nums2{
if (nums1 == nil || nums1.count == 0) return 0;
if (nums2 == nil || nums2.count == 0) return 0;
//dp[i][j]:num1[i-1] 和 num2[j-1] 最长公共子序列的长度
//只用2行:上一行 当前行
NSMutableArray<NSMutableArray*> * dp = [NSMutableArray array];
for (int row = 0; row<=1; row++) {
dp[row] = [NSMutableArray array];
for (int col = 0; col <= nums2.count; col++) {
dp[row][col] = @(0);
}
}
for (int row = 1; row <= nums1.count; row++) {
int preRow = (row-1) % 2;
int curRow = row % 2;
for (int col = 1; col <= nums2.count; col++) {
//状态转移方程
if ([nums1[row-1] intValue] == [nums2[col-1] intValue]) {
dp[curRow][col] = @([dp[preRow][col-1] intValue] + 1);
}else{
int length1 = [dp[curRow][col-1] intValue];
int length2 = [dp[preRow][col] intValue];
dp[curRow][col] = @(MAX(length1, length2));
}
}
}
return [dp[nums1.count % 2][nums2.count] intValue];
}
四、非递归实现(一维数组)
可以将 二维数组 优化成 一维数组,进一步降低空间复杂度
+(int)lcs4nums1:(NSArray*)nums1 nums2:(NSArray*)nums2{
if (nums1 == nil || nums1.count == 0) return 0;
if (nums2 == nil || nums2.count == 0) return 0;
//dp[i][j]:num1[i-1] 和 num2[j-1] 最长公共子序列的长度
//只用一维数组
NSMutableArray * dp = [NSMutableArray array];
for (int col = 0; col <= nums2.count; col++) {
dp[col] = @(0);
}
for (int row = 1; row <= nums1.count; row++) {
int cur = 0;
for (int col = 1; col <= nums2.count; col++) {
int leftTop = cur;
cur = [dp[col] intValue];//记录当前值,作为下一轮的leftTop
//状态转移方程
if ([nums1[row-1] intValue] == [nums2[col-1] intValue]) {
dp[col] = @(leftTop + 1);
}else{
int length1 = [dp[col-1] intValue]; //左面
int length2 = [dp[col] intValue]; //上面
dp[col] = @(MAX(length1, length2)); //覆盖
}
}
}
return [dp[nums2.count] intValue];
}
五、非递归实现(一维数组-使用较短的序列)
可以空间复杂度优化至 O(k) , k = min{n, m}
+(int)lcs5nums1:(NSArray*)nums1 nums2:(NSArray*)nums2{
if (nums1 == nil || nums1.count == 0) return 0;
if (nums2 == nil || nums2.count == 0) return 0;
//取出较短的数组作为列
NSArray * rowNums = nums1;
NSArray * colNums = nums2;
if (nums1.count < nums2.count) {
colNums = nums1;
rowNums = nums2;
}
//dp[i][j]:num1[i-1] 和 num2[j-1] 最长公共子序列的长度
//只用一维数组
NSMutableArray * dp = [NSMutableArray array];
for (int col = 0; col <= colNums.count; col++) {
dp[col] = @(0);
}
for (int row = 1; row <= rowNums.count; row++) {
int cur = 0;
for (int col = 1; col <= colNums.count; col++) {
int leftTop = cur;
cur = [dp[col] intValue];//记录当前值,作为下一轮的leftTop
//状态转移方程
if ([rowNums[row-1] intValue] == [colNums[col-1] intValue]) {
dp[col] = @(leftTop + 1);
}else{
int length1 = [dp[col-1] intValue]; //左面
int length2 = [dp[col] intValue]; //上面
dp[col] = @(MAX(length1, length2)); //覆盖
}
}
}
return [dp[colNums.count] intValue];
}
行者常至,为者常成!
