目录
最长公共子串(Longest Common Substring)
一、最长公共子串 - 题目
最长公共子串(Longest Common Substring)
子串是连续的子序列
求两个字符串的最长公共子串长度
ABCBA 和 BABCA 的最长公共子串是 ABC,长度为 3
二、最长公共子串 – 思路
假设 2 个字符串分别是 str1、str2
i ∈ [1, str1.length]
j ∈ [1, str2.length]
假设 dp(i, j) 是以 str1[i – 1]、str2[j – 1] 结尾的最长公共子串长度
dp(i, 0)、dp(0, j) 初始值均为 0
如果 str1[i – 1] = str2[j – 1],那么 dp(i, j) = dp(i – 1, j – 1) + 1
如果 str1[i – 1] ≠ str2[j – 1],那么 dp(i, j) = 0
最长公共子串的长度是所有 dp(i, j) 中的最大值 max { dp(i, j) }
三、最长公共子串 – 实现
/// 返回最长公共子串长度
/// @param str1 串1
/// @param str2 串2
+(int)lcSubstringWithString1:(NSString*)str1 string2:(NSString*)str2{
if (str1 == nil || str1.length == 0) return 0;
if (str2 == nil || str2.length == 0) return 0;
//dp[i][j] str1[i-1] str[j-1] 的最长公共子串长度
NSMutableArray<NSMutableArray*> * dp = [NSMutableArray array];
for (int i=0; i<=str1.length; i++) {
dp[i] = [NSMutableArray array];
for (int j = 0; j<=str2.length; j++) {
dp[i][j] = @(0);
}
}
int max = 0;
for (int i = 1; i<=str1.length; i++) {
for (int j = 1; j<=str2.length; j++) {
// if ([str1 characterAtIndex:i-1] == [str2 characterAtIndex:j-1]) {
// dp[i][j] = @([dp[i-1][j-1] intValue]+1);
// }else{
// dp[i][j] = @(0);
// }
if ([str1 characterAtIndex:i-1] != [str2 characterAtIndex:j-1]) continue;
int n = [dp[i-1][j-1] intValue]+1;
dp[i][j] = @(n);
max = MAX(max, n);
}
}
return max;
}
空间复杂度:O(n ∗ m)
时间复杂度:O(n ∗ m)
dp 数组的计算结果如下所示
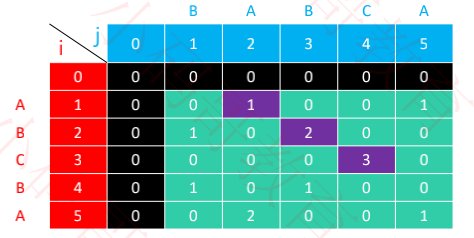
四、最长公共子串 – 一维数组实现
1、实现方式一
+(int)lcSubstring2WithString1:(NSString*)str1 string2:(NSString*)str2{
if (str1 == nil || str1.length == 0) return 0;
if (str2 == nil || str2.length == 0) return 0;
//dp[j] str1[i-1] str[j-1] 的最长公共子串长度 二维数组优化成一维数组
NSMutableArray * dp = [NSMutableArray array];
for (int j = 0; j<=str2.length; j++) {
dp[j] = @(0);
}
int max = 0;
for (int i = 1; i<=str1.length; i++) {
int cur = 0;
for (int j = 1; j<=str2.length; j++) {
int leftTop = cur;
cur = [dp[j] intValue];
if ([str1 characterAtIndex:i-1] != [str2 characterAtIndex:j-1]){
dp[j] = @(0);
}else{
int n = leftTop+1;
dp[j] = @(n);
max = MAX(max, n);
}
}
}
return max;
}
2、实现方式二(优化)
+(int)lcSubstring3WithString1:(NSString*)str1 string2:(NSString*)str2{
if (str1 == nil || str1.length == 0) return 0;
if (str2 == nil || str2.length == 0) return 0;
//dp[j] str1[i-1] str[j-1] 的最长公共子串长度 二维数组优化成一维数组
NSMutableArray * dp = [NSMutableArray array];
for (int j = 0; j<=str2.length; j++) {
dp[j] = @(0);
}
int max = 0;
for (int i = 1; i<=str1.length; i++) {
for (int j =(int)str2.length; j>=1; j--) {
if ([str1 characterAtIndex:i-1] != [str2 characterAtIndex:j-1]){
dp[j] = @(0);
}else{
int n = [dp[j-1] intValue]+1;
dp[j] = @(n);
max = MAX(max, n);
}
}
}
return max;
}
3、实现方式三(进一步优化)
+(int)lcSubstring4WithString1:(NSString*)str1 string2:(NSString*)str2{
if (str1 == nil || str1.length == 0) return 0;
if (str2 == nil || str2.length == 0) return 0;
NSString * rowStr = str1;
NSString * colStr = str2;
if (str1.length < str2.length) {
rowStr = str2;
colStr = str1;
}
//dp[j] str1[i-1] str[j-1] 的最长公共子串长度 二维数组优化成一维数组
//长度短的做列,减少空间占用
NSMutableArray * dp = [NSMutableArray array];
for (int col = 0; col<=colStr.length; col++) {
dp[col] = @(0);
}
int max = 0;
for (int row = 1; row<=rowStr.length; row++) {
for (int col =(int)colStr.length; col>=1; col--) {
if ([rowStr characterAtIndex:row-1] != [colStr characterAtIndex:col-1]){
dp[col] = @(0);
}else{
int n = [dp[col-1] intValue]+1;
dp[col] = @(n);
max = MAX(max, n);
}
}
}
return max;
}
空间复杂度:O(k) , k = min{n, m}
时间复杂度:O(n ∗ m)
0-1背包
一、背包-题目
有 n 件物品和一个最大承重为 W 的背包,每件物品的重量是 𝑤i、价值是 𝑣i
在保证总重量不超过 W 的前提下,选择某些物品装入背包,背包的最大总价值是多少?
注意:每个物品只有 1 件,也就是每个物品只能选择 0 件或者 1 件
二、思路
假设 values 是价值数组,weights 是重量数组
编号为 k 的物品,价值是 values[k],重量是 weights[k],k ∈ [0, n)
假设 dp(i, j) 是 有前 i 件物品可选,最大承重为 j 时的最大总价值,i ∈ [1, n],j ∈ [1, W]
dp(i, 0)、dp(0, j) 初始值均为 0
分为两种情况,最后一件物品能够装下,不能够装下:
如果 j < weights[i – 1] 不能够装下:
那么 dp(i, j) = dp(i – 1, j)
如果 j ≥ weights[i – 1] 能够装下:
选择装入: value1 = dp(i – 1, j – weights[i – 1]) + values[i – 1]
选择不装: value2 = dp(i – 1, j)
那么 dp(i, j) = max { value1,value2 } 。
三、代码实现
1、暴力递归实现
/// 0-1背包问题(背包装的物品的最大价值)
/// @param values 价值数组
/// @param weights 重量数组,与价值数组一一对应,表示同一件物品
/// @param capacity 背包容量
//暴力递归实现
+(int)knapsackWithValues:(NSArray*)values
weights:(NSArray*)weights
capacity:(int)capacity{
if (values == nil || values.count == 0) return 0;
if (weights == nil || weights.count == 0) return 0;
if (capacity < 1 || values.count != weights.count) return 0;
return [self __knapsackWithValues:values
weights:weights
capacity:capacity
frontN:(int)weights.count];
}
+(int)__knapsackWithValues:(NSArray*)values
weights:(NSArray*)weights
capacity:(int)capacity
frontN:(int)n{
if(n < 1) return 0;
if (capacity < 1) return 0;
//最后一件不可选
int value = 0;
if (capacity < [weights[n-1] intValue]) {
//最大承重:capacity,
//前i 件:n-1
//的最大价值
value = [self __knapsackWithValues:values
weights:weights
capacity:capacity
frontN:n-1];
//最后一件可选
}else{
//最大承重为:capacity - 最后一件重量,
//前i件 :n-1
//的最大价值
int value1 = [self __knapsackWithValues:values
weights:weights
capacity:capacity - [weights[n-1] intValue]
frontN:n-1];
//最大承重为:capacity,
//前i件 :n
//的最大价值
value1 = value1 + [values[n-1] intValue];
//最大承重:capacity,
//前i 件:n-1
//的最大价值
int value2 = [self __knapsackWithValues:values
weights:weights
capacity:capacity
frontN:n-1];
value = MAX(value1, value2);
}
return value;
}
二、非递归实现 - 二维数组
dp 数组的计算结果如下所示
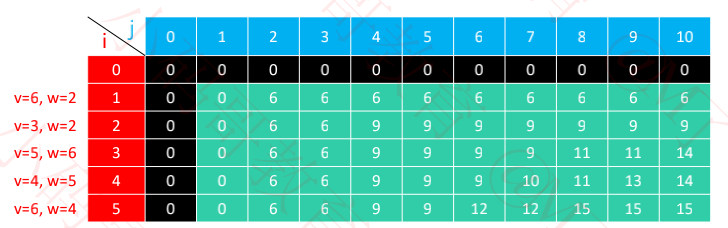
+(int)knapsack2WithValues:(NSArray*)values
weights:(NSArray*)weights
capacity:(int)capacity{
if (values == nil || values.count == 0) return 0;
if (weights == nil || weights.count == 0) return 0;
if (capacity < 1 || values.count != weights.count) return 0;
//dp[i][j] 前i个物品,最大承重为j 的最大价值
NSMutableArray<NSMutableArray*> * dp = [NSMutableArray array];
for (int i = 0; i<=weights.count; i++) {
dp[i] = [NSMutableArray array];
for (int j = 0; j<=capacity; j++) {
dp[i][j] = @(0);
}
}
//状态转移方程
for (int i = 1; i<=weights.count; i++) {
for (int j = 1; j<=capacity; j++) {
if (j < [weights[i-1] intValue]) {//不可装
dp[i][j] = dp[i-1][j];
}else{//可装
//可装 - 并且选择装入
int value1 = [dp[i-1][j-[weights[i-1] intValue]] intValue];
value1 += [values[i-1] intValue];
//可装 - 但是选择不装
int value2 = [dp[i-1][j] intValue];
dp[i][j] = @(MAX(value1, value2));
}
}
}
return [dp[weights.count][capacity] intValue];
}
三、非递归实现 - 一维数组
dp(i, j) 都是由 dp(i – 1, k) 推导出来的,也就是说,第 i 行的数据是由它的上一行第 i – 1 行推导出来的
因此,可以使用一维数组来优化
另外,由于 k ≤ j ,所以 j 的遍历应该由大到小,否则导致数据错乱
+(int)knapsack3WithValues:(NSArray*)values
weights:(NSArray*)weights
capacity:(int)capacity{
if (values == nil || values.count == 0) return 0;
if (weights == nil || weights.count == 0) return 0;
if (capacity < 1 || values.count != weights.count) return 0;
//dp[i][j] 前i个物品,最大承重为j 的最大价值
NSMutableArray<NSNumber*> * dp = [NSMutableArray array];
for (int j = 0; j<=capacity; j++) {
dp[j] = @(0);
}
//状态转移方程
for (int i = 1; i<=weights.count; i++) {
// 下面这种写法不可行
// int cur = 0;
// for (int j = 1; j<=capacity; j++) {
// if (j < [weights[i-1] intValue]) {//不可装
// dp[j] = dp[j];
// }else{//可装
// #warning 这样写是不行了 dp[j-weights[i-1] 的值已经被覆盖 拿不到了
// int leftTop = cur;
// cur = [dp[j - [weights[i-1] intValue] + 1] intValue];//注意此处的位置
//
// //可装 - 并且选择装入
// int value1 = leftTop + [values[i-1] intValue];
// //可装 - 但是选择不装
// int value2 = [dp[j] intValue];
// dp[j] = @(MAX(value1, value2));
// }
// }
for (int j = capacity; j>=1; j--) {
if (j < [weights[i-1] intValue]) {//不可装
dp[j] = dp[j];
}else{//可装
//可装 - 并且选择装入
int value0 = [dp[j - [weights[i-1] intValue]] intValue];
int value1 = value0 + [values[i-1] intValue];
//可装 - 但是选择不装
int value2 = [dp[j] intValue];
dp[j] = @(MAX(value1, value2));
}
}
}
return dp[capacity].intValue;
}
四、非递归实现 - 一维数组(优化)
观察二维数组表,得出结论:j 的下界可以从 1 改为 weights[i – 1]
+(int)knapsack4WithValues:(NSArray*)values
weights:(NSArray*)weights
capacity:(int)capacity{
if (values == nil || values.count == 0) return 0;
if (weights == nil || weights.count == 0) return 0;
if (capacity < 1 || values.count != weights.count) return 0;
//dp[i][j] 前i个物品,最大承重为j 的最大价值
NSMutableArray<NSNumber*> * dp = [NSMutableArray array];
for (int j = 0; j<=capacity; j++) {
dp[j] = @(0);
}
//状态转移方程(优化)
// for (int i = 1; i<=weights.count; i++) {
// for (int j = capacity; j>=1; j--) {
// if (j < [weights[i-1] intValue]) continue;
// //可装 - 并且选择装入
// int value0 = [dp[j - [weights[i-1] intValue]] intValue];
// int value1 = value0 + [values[i-1] intValue];
// //可装 - 但是选择不装
// int value2 = [dp[j] intValue];
// dp[j] = @(MAX(value1, value2));
// }
// }
//状态转移方程(再优化)
for (int i = 1; i<=weights.count; i++) {
for (int j = capacity; j>=[weights[i-1] intValue]; j--) {
//可装 - 并且选择装入
int value0 = [dp[j - [weights[i-1] intValue]] intValue];
int value1 = value0 + [values[i-1] intValue];
//可装 - 但是选择不装
int value2 = [dp[j] intValue];
dp[j] = @(MAX(value1, value2));
}
}
return dp[capacity].intValue;
}
0-1背包,恰好装满
有 n 件物品和一个最大承重为 W 的背包,每件物品的重量是 𝑤i、价值是 𝑣i
在保证总重量恰好等于 W 的前提下,选择某些物品装入背包,背包的最大总价值是多少?
注意:每个物品只有 1 件,也就是每个物品只能选择 0 件或者 1 件
dp(i, j) 初始状态调整
dp(i, 0) = 0,总重量恰好为 0,最大总价值必然也为 0
dp(0, j) = –∞(负无穷),j ≥ 1,负数在这里代表无法恰好装满
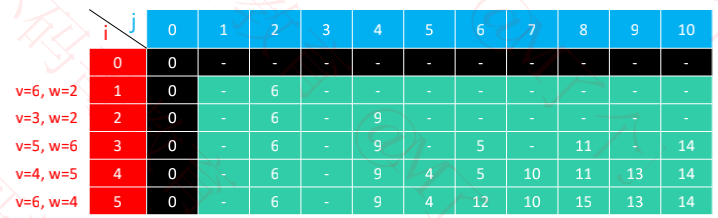
/// 恰好装满时的最大价值(-1代表无法装满)
/// @param values 价值数组
/// @param weights 重量数组,与价值数组一一对应,表示同一件物品
/// @param capacity 背包容量
+(int)knapsack5WithValues:(NSArray*)values
weights:(NSArray*)weights
capacity:(int)capacity{
if (values == nil || values.count == 0) return -1;
if (weights == nil || weights.count == 0) return -1;
if (capacity < 1 || values.count != weights.count) return 0;
//dp[i][j] 前i个物品,最大承重为j 的最大价值
NSMutableArray<NSNumber*> * dp = [NSMutableArray array];
dp[0] = @(0);//0
for (int j = 0; j<=capacity; j++) {
dp[j] = @(INT_MIN);//负无穷
}
//状态转移方程(再优化)
for (int i = 1; i<=weights.count; i++) {
for (int j = capacity; j>=[weights[i-1] intValue]; j--) {
//可装 - 并且选择装入
int value0 = [dp[j - [weights[i-1] intValue]] intValue];
int value1 = value0 + [values[i-1] intValue];
//可装 - 但是选择不装
int value2 = [dp[j] intValue];
dp[j] = @(MAX(value1, value2));
}
}
return dp[capacity].intValue < 0 ? -1 : dp[capacity].intValue;
}
行者常至,为者常成!
