【进阶】22、跳表

2014-03-22 | 阅读：

跳表(SkipList)

一、思考

一个有序链表搜索、添加、删除的平均时间复杂度是多少？
O(n)

能否利用二分搜索优化有序链表，将搜索、添加、删除的平均时间复杂度降低至 O(logn)？
链表没有像数组那样的高效随机访问（O(1) 时间复杂度），所以不能像有序数组那样直接进行二分搜索优化
那有没有其他办法让有序链表搜索、添加、删除的平均时间复杂度降低至 O(logn)？
使用跳表（SkipList）

二、跳表

跳表，又叫做跳跃表、跳跃列表，在有序链表的基础上增加了“跳跃”的功能
由William Pugh于1990年发布，设计的初衷是为了取代平衡树（比如红黑树）
Redis中的 SortedSet、LevelDB 中的 MemTable 都用到了跳表
Redis、LevelDB 都是著名的 Key-Value 数据库

对比平衡树
跳表的实现和维护会更加简单
跳表的搜索、删除、添加的平均时间复杂度是 O(logn)

三、使用跳表优化链表

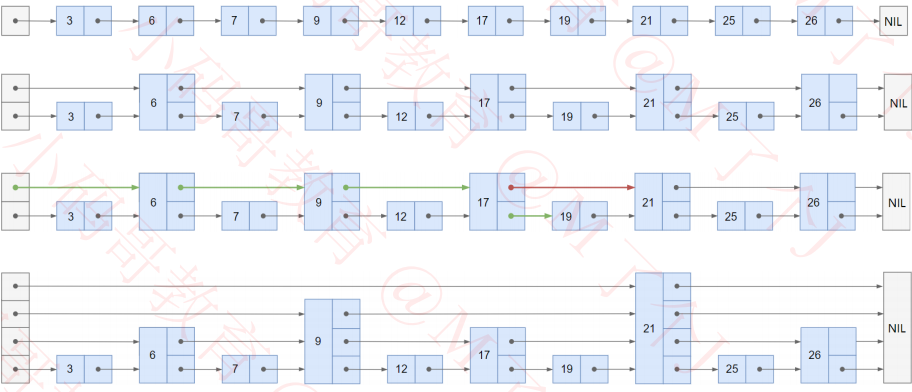
跳表实现

一、跳表的接口设计

/// 创建一个跳表实例
+(instancetype)skipList;


/// 创建一个跳表实例
/// @param comparator 比较器
+(instancetype)skipListWithComparator:(nullable LCCompareBlock)comparator;


/// 跳表的长度
-(int)size;


/// 跳表是否为空
-(BOOL)isEmpty;


/// 跳表搜索，返回key对应的value
/// @param key 键
-(id)get:(id)key;


/// 添加键值对，返回nil或旧value
/// @param key 键
/// @param value 值
-(id)putKey:(id)key value:(id)value;


/// 移除键值对，返回移除的value
/// @param key 键值
-(id)remove:(id)key;

二、跳表的搜索

① 从顶层链表的首元素开始，从左往右搜索，直至找到一个大于或等于目标的元素，或者到达当前层链表的尾部
② 如果该元素等于目标元素，则表明该元素已被找到
③ 如果该元素大于目标元素或已到达链表的尾部，则退回到当前层的前一个元素，然后转入下一层进行搜索

/// 跳表搜索，返回key对应的value
/// @param key 键
-(id)get:(id)key{
    [self __keyCheck:key];
    
    LCSKNode * node = self.first;
    for (int level = self.level-1; level>=0; level--) {
        int cmp = -1;
        
        while (node.nexts[level]&&
               (cmp = [self __compareValue1:key
                                     value2:node.nexts[level]]) > 0) {
            
            node = node.nexts[level];
        }
        
        //node.next[level] = key
        if (cmp == 0) return node.nexts[level].value;
        
        //node.next[level] > key||node.next[level] == nil
        // 来到下一层
    }
   
    //没有找到，返回nil
    return nil;
}

三、跳表的添加、删除

添加的细节
随机决定新添加元素的层数

/// 添加键值对，返回nil或旧value
/// @param key 键
/// @param value 值
-(id)putKey:(id)key value:(id)value{
    [self __keyCheck:key];
    
    //用于存放返回的节点
    NSMutableArray * preNodes = [NSMutableArray array];
    for (int i = 0; i<self.level; i++) {
        [preNodes addObject:null];
    }
    
    LCSKNode * node = self.first;
    for (int levelIdx = self.level-1; levelIdx>=0; levelIdx--) {
        int cmp = -1;
        
        while (node.nexts[levelIdx] != null &&
               (cmp = [self __compareValue1:key
                                     value2:node.nexts[levelIdx].key]) > 0) {
            node = node.nexts[levelIdx];
        }
        
        
        if (cmp == 0) {//node.next[levelIdx].key = key
            id oldValue =  node.nexts[levelIdx].value;
            node.nexts[levelIdx].value = value;
            return oldValue;
        }
        
        //node.next[levelIdx].key > key || node.next[levelIdx].key == null
        //记录进入下一层的是哪个节点
        preNodes[levelIdx] = node;
       
        
        //来到下一层
    }
    
    
    //没有找到，创建新节点，并返回nil
    int newNodeLevel = [self __randomLevel];
    LCSKNode * newNode = [LCSKNode nodeWithKey:key value:value level:newNodeLevel];
    
    /**
     newNodeLevel < self.level
     newNodeLevel >= self.level
     从 0 层 开始
     */
    for (int levelIdx = 0; levelIdx < newNodeLevel; levelIdx++) {
        
        if (levelIdx >= self.level){
            self.first.nexts[levelIdx] = newNode;
        }else{
            LCSKNode * preNode = preNodes[levelIdx];
            newNode.nexts[levelIdx] = preNode.nexts[levelIdx];
            preNode.nexts[levelIdx] = newNode;
        }
    }
    
    //跟新节点数量
    self.size++;
    
    //更新当前有效层数
    self.level = MAX(self.level, newNodeLevel);
    
    return nil;
}

#define MAX_LEVEL (32)  //最大层高
#define P (0.25)        //层数概率


/// 随机获取层数
-(int)__randomLevel{
    int level = 1;
//    double randomP = (random()%100 * 1.0)/100;//[0 0.99]
    while (((random()%100 * 1.0)/100) < P && level <MAX_LEVEL) {
        level++;
    }
    return level;
}

删除的细节
删除一个元素后，整个跳表的层数可能会降低

/// 移除键值对，返回移除的value
/// @param key 键值
-(id)remove:(id)key{
    [self __keyCheck:key];
    
    //用于存放返回的节点
    NSMutableArray * preNodes = [NSMutableArray array];
    for (int i = 0; i<self.level; i++) {
        [preNodes addObject:null];
    }
    
    BOOL exist = false;
    
    LCSKNode * node = self.first;
    for (int levelIdx = self.level-1; levelIdx>=0; levelIdx--) {
        int cmp = -1;
        
        while (node.nexts[levelIdx] != null &&
               (cmp = [self __compareValue1:key
                                     value2:node.nexts[levelIdx].key]) > 0) {
            node = node.nexts[levelIdx];
        }
        
        preNodes[levelIdx] = node;
        if (cmp == 0) {exist = true;}
    }

    if (exist == false) return nil;
    
    //需要被删除的节点
    LCSKNode * removeNode = node.nexts[0];
    
    for (int i = 0; i<removeNode.nexts.count; i++) {
        LCSKNode * preNode = preNodes[i];
        preNode.nexts[i] = preNode.nexts[i].nexts[i];
    }
    
    
    //跟新节点数量
    self.size--;
    
    //更新当前有效层数
    while (self.level>0 && self.first.nexts[self.level-1] == null) {
        self.level--;
    }
    
    
    return removeNode.value;
}

跳表的层数

跳表是按层构造的，底层是一个普通的有序链表，高层相当于是低层的“快速通道”
在第 i 层中的元素按某个固定的概率 p（通常为 ½ 或 ¼ ）出现在第 i + 1层中，产生越高的层数，概率越低
✓ 元素层数恰好等于 1 的概率为 1 – p
✓ 元素层数大于等于 2 的概率为 p，而元素层数恰好等于 2 的概率为 p * (1 – p)
✓ 元素层数大于等于 3 的概率为 p^2，而元素层数恰好等于 3 的概率为 p^2 * (1 – p)
✓ 元素层数大于等于 4 的概率为 p^3，而元素层数恰好等于 4 的概率为 p^3 * (1 – p)
✓ ……
✓ 一个元素的平均层数是 1 / (1 – p)

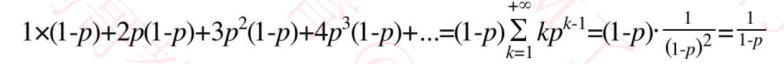
当 p = ½ 时，每个元素所包含的平均指针数量是 2
当 p = ¼ 时，每个元素所包含的平均指针数量是 1.33

跳表的复杂度分析

每一层的元素数量
第 1 层链表固定有 n 个元素
第 2 层链表平均有 n * p 个元素
第 3 层链表平均有 n * p^2 个元素
第 k 层链表平均有 n * p^k 个元素
…

另外
最高层的层数是 log((1/p)^n)，平均有个 1/p 元素
在搜索时，每一层链表的预期查找步数最多是 1/p，所以总的查找步数是 –(logp^(n/p))，时间复杂度是O(logn)

行者常至，为者常成！

JHHK