目录
串(Sequence)
一、介绍
本课程研究的串是开发中非常熟悉的字符串,是由若干个字符组成的有限序列
| String Text = “thank” | t | h | a | n | k |
字符串 thank 的前缀(prefix)、真前缀(proper prefix)、后缀(suffix)、真后缀(proper suffix)
| 前缀 | t | th, | tha | than | thank |
| 真前缀 | t | th | tha | than | |
| 后缀 | thank | hank | ank | nk | k |
| 真后缀 | hank | ank | nk | k |
二、串匹配算法
本课程主要研究串的匹配问题,比如
查找一个模式串(Pattern)在文本串(Text)中的位置
String text = "Hello World";
String patter = "or";
text.indexOf(patter);//7
text.indexOf("other");//-1
几个经典的串匹配算法
蛮力(Brute Force)
KMP
Boyer-Moore
Rabin-Karp
Sunday
本课程用 tlen 代表文本串 Text 的长度,plen 代表模式串 Pattern 的长度
蛮力(Brute Force
以字符为单位,从左到右移动模式串,直到匹配成功
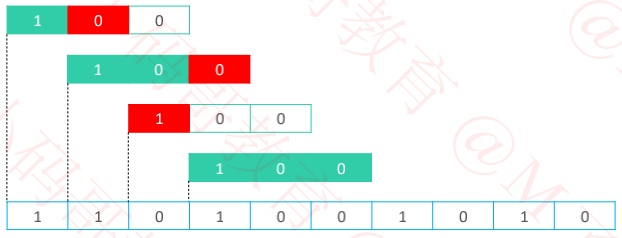
蛮力算法有 2 种常见实现思路
一、实现思路一
1、步骤一
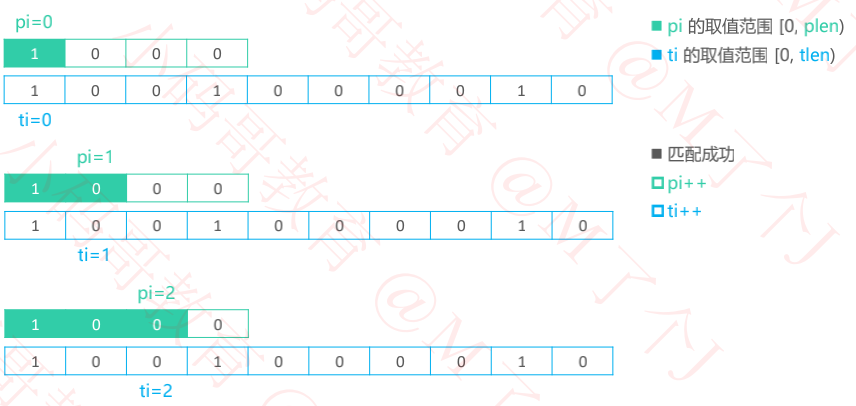
2、步骤二

3、代码实现
-(int)indexOfText:(NSString*)text pattern:(NSString*)patter{
if (text == nil ||patter == nil) return -1;
int tlen = (int)text.length , plen = (int)patter.length;
if (tlen == 0 || plen == 0 || plen > tlen) return -1;
int ti = 0 , pi = 0;
while (ti < tlen && pi < plen) {
char t = [text characterAtIndex:ti];
char p = [patter characterAtIndex:pi];
if (t == p) {
ti++;
pi++;
}else{
ti -= pi-1;
pi = 0;
}
}
//ti == tlen || pi == plen
return (pi == plen) ? (ti - pi) : -1;
}
4、代码优化
此前实现的蛮力算法,在恰当的时候可以提前退出,减少比较次数
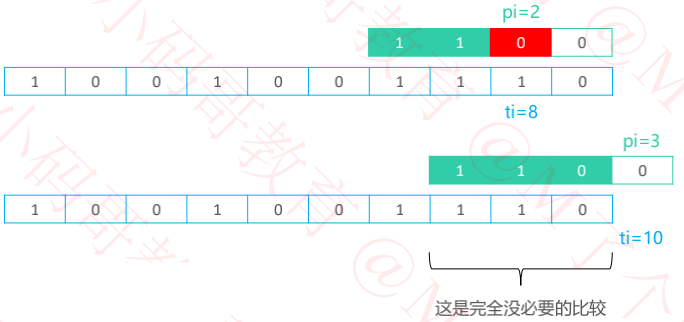
因此,ti 的退出条件可以从 ti < tlen 改为
ti – pi <= tlen – plen
ti – pi 是指每一轮比较中 Text 首个比较字符的位置
-(int)indexOf2Text:(NSString*)text pattern:(NSString*)patter{
if (text == nil ||patter == nil) return -1;
int tlen = (int)text.length , plen = (int)patter.length;
if (tlen == 0 || plen == 0 || plen > tlen) return -1;
int ti = 0 , pi = 0 ,lenDelta = tlen - plen;
while (ti-pi <= lenDelta && pi < plen) {
char t = [text characterAtIndex:ti];
char p = [patter characterAtIndex:pi];
if (t == p) {
ti++;
pi++;
}else{
ti -= pi-1;
pi = 0;
}
}
//ti == tlen || pi == plen
return (pi == plen) ? (ti - pi) : -1;
}
二、实现思路二
1、步骤一

2、步骤二

3、代码实现
-(int)indexOfText:(NSString*)text pattern:(NSString*)patter{
if (text == nil ||patter == nil) return -1;
int tlen = (int)text.length , plen = (int)patter.length;
if (tlen == 0 || plen == 0 || plen > tlen) return -1;
int tiMax = tlen - plen;
for (int ti = 0; ti <= tiMax; ti++) {
int pi = 0;
for (;pi < plen;pi++) {
if ([text characterAtIndex:ti+pi] != [patter characterAtIndex:pi]) break;
}
if (pi == plen) return ti;
}
return -1;
}
三、性能分析
n 是文本串长度,m 是模式串长度
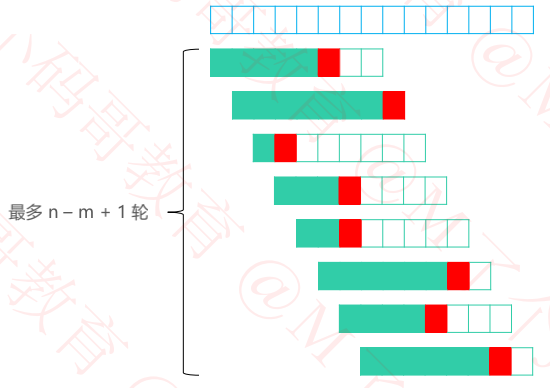
最好情况
只需一轮比较就完全匹配成功,比较 m 次( m 是模式串的长度)
时间复杂度为 O(m)
最坏情况(字符集越大,出现概率越低)
执行了 n – m + 1 轮比较( n 是文本串的长度)
每轮都比较至模式串的末字符后失败( m – 1 次成功,1 次失败)
时间复杂度为 O(m ∗ (n − m + 1)),由于一般 m 远小于 n,所以为 O(nm)

KMP
KMP 是 Knuth–Morris–Pratt 的简称(取名自3位发明人的名字),于1977年发布
Donald Knuth 、 James Hiram Morris 、 Vaughan Pratt
一、蛮力 VS KMP
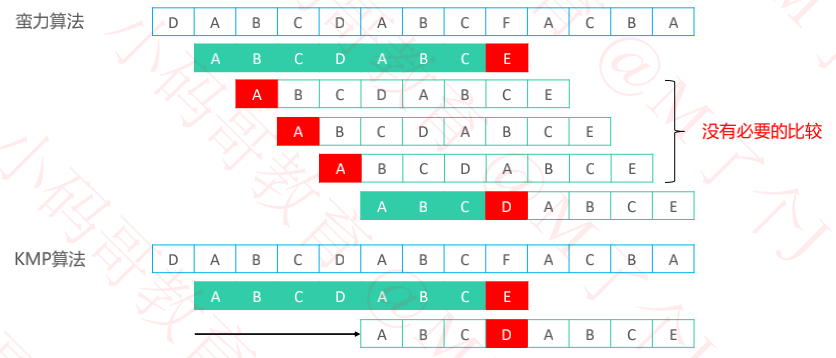
对比蛮力算法,KMP的精妙之处:充分利用了此前比较过的内容,可以很聪明地跳过一些不必要的比较位置
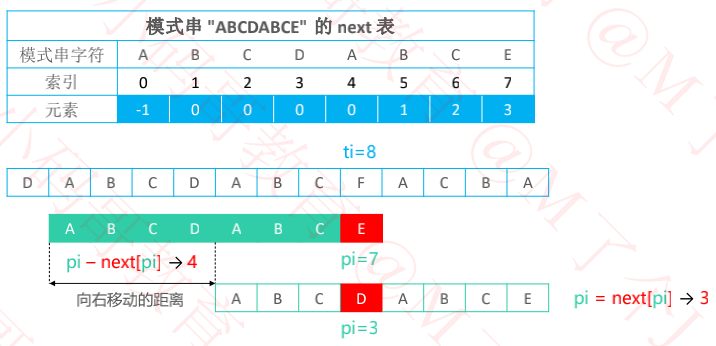
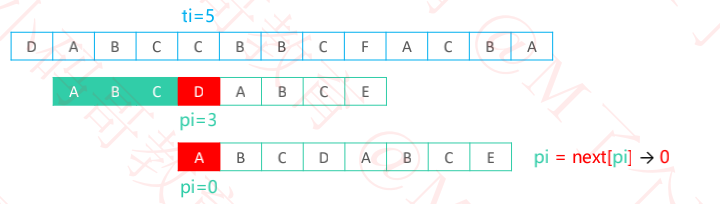
二、next表的使用
KMP 会预先根据模式串的内容生成一张 next 表(一般是个数组)
三、核心原理

当 d、e 失配时,如果希望 Pattern 能够一次性向右移动一大段距离,然后直接比较 d、c 字符
前提条件是 A 必须等于 B
所以 KMP 必须在失配字符 e 左边的子串中找出符合条件的 A、B,从而得知向右移动的距离
向右移动的距离:e左边子串的长度 – A的长度,
等价于:e的索引 – c的索引 且 c的索引 == next[e的索引],
所以向右移动的距离:e的索引 – next[e的索引]
总结
如果在 pi 位置失配,向右移动的距离是 pi – next[pi],所以 next[pi] 越小,移动距离越大
next[pi] 是 pi 左边子串的 真前缀真后缀的最大公共子串长度
四、真前缀、真后缀的最大公共子串长度 及 next表
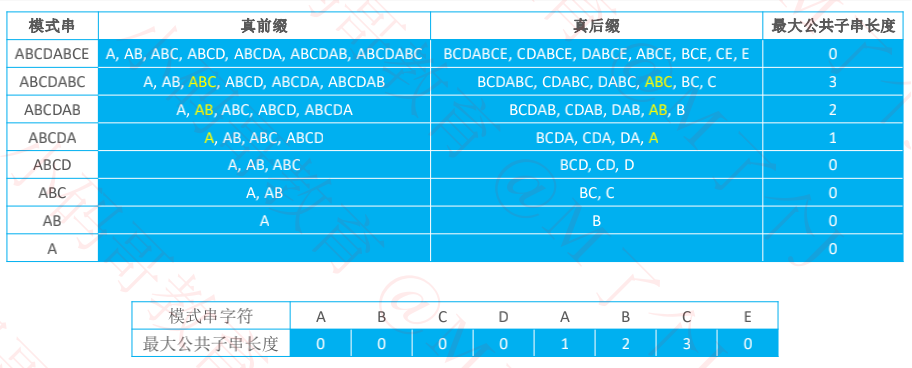
将最大公共子串长度都向后移动 1 位,首字符设置为 负1,就得到了 next 表
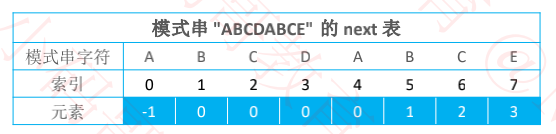
五、负 1的精妙之处
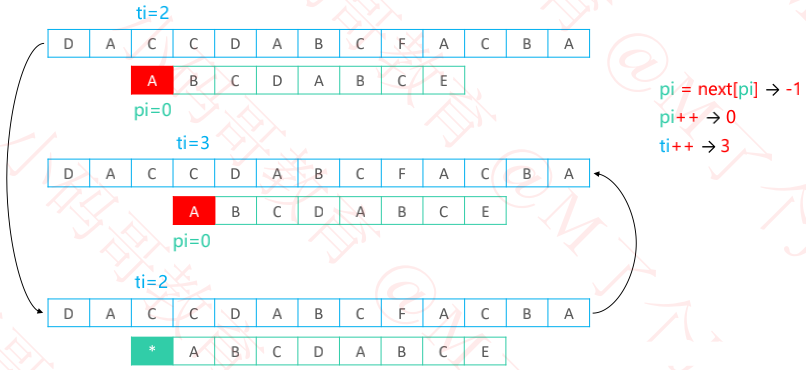
相当于在负1位置有个假想的通配字符(哨兵)
匹配成功后 ti++、pi++
六、主算法实现
-(int)indexOfText:(NSString*)text pattern:(NSString*)patter{
if (text == nil ||patter == nil) return -1;
int tlen = (int)text.length , plen = (int)patter.length;
if (tlen == 0 || plen == 0 || plen > tlen) return -1;
//拿到next表
NSArray * next = [self getNextTable:patter];
int ti = 0 , pi = 0;
while (ti - pi <= tlen - plen && pi < plen) {
char t = [text characterAtIndex:ti];
char p = [patter characterAtIndex:pi];
//相等 或 pi == -1 时
if (t == p || pi < 0) {
ti++;
pi++;
}else{
//从next表中拿到下次比对的位置
pi = [next[pi] intValue];
}
}
return pi == plen ? ti - pi : -1;
}
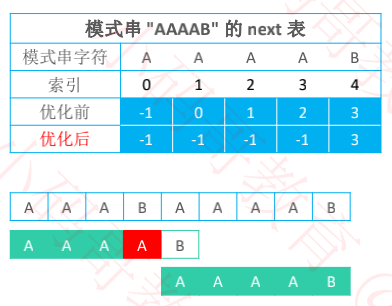
七、KMP – 为什么是“最大“公共子串长度?
假设文本串是AAAAABCDEF,模式串是AAAAB

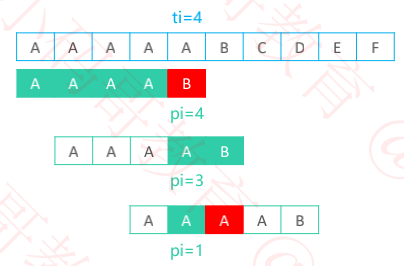
应该将1、2、3中的哪个值赋值给 pi 是正确的?
将 3 赋值给 pi
向右移动了 1 个字符单位,最后成功匹配
将 1 赋值给 pi
向右移动了 3 个字符单位,错过了成功匹配的机会
公共子串长度越小,向右移动的距离越大,越不安全
公共子串长度越大,向右移动的距离越小,越安全
KMP - next表
一、KMP – next表的构造思路

已知 next[i] == n
①如果 Pattern[i] == Pattern[n]
那么 next[i + 1] == n + 1
②如果 Pattern[i] != Pattern[n]
已知 next[n] == k
如果 Pattern[i] == Pattern[k]
✓ 那么 next[i + 1] == k + 1
如果 Pattern[i] != Pattern[k]
✓ 将 k 代入 n ,重复执行 ②
-(NSArray<NSNumber*>*)getNextTable:(NSString*)patter{
NSMutableArray<NSNumber*> * next = [NSMutableArray array];
int i = 0;
int n = -1;
next[0] = @(-1);
int iMax = (int)patter.length - 1;
while (i < iMax) {
char ichar = [patter characterAtIndex:i];
char nchar = [patter characterAtIndex:n];
if (n < 0 || ichar == nchar){
next[++i] = @(++n);
}else{
n = next[n].intValue;
}
}
return next;
}
二、next表的优化思路
已知:next[i] == n,next[n] == k
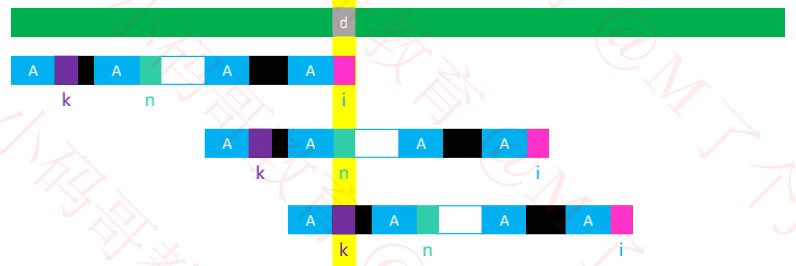
如果 Pattern[i] != d,就让模式串滑动到 next[i](也就是n)位置跟 d 进行比较
如果 Pattern[n] != d,就让模式串滑动到 next[n](也就是k)位置跟 d 进行比较
如果 Pattern[i] == Pattern[n],那么当 i 位置失配时,模式串最终必然会滑到 k 位置跟 d 进行比较
所以 next[i] 直接存储 next[n](也就是k)即可
-(NSArray<NSNumber*>*)getNextTable2:(NSString*)patter{
NSMutableArray<NSNumber*> * next = [NSMutableArray array];
int i = 0;
int n = -1;
next[0] = @(-1);
int iMax = (int)patter.length - 1;
while (i < iMax) {
char ichar = [patter characterAtIndex:i];
char nchar = [patter characterAtIndex:n];
if (n < 0 || ichar == nchar){
i++;
n++;
ichar = [patter characterAtIndex:i];
nchar = [patter characterAtIndex:n];
if (ichar == nchar) {
next[i] = next[n];
}else{
next[i] = @(n);
}
}else{
n = next[n].intValue;
}
}
return next;
}
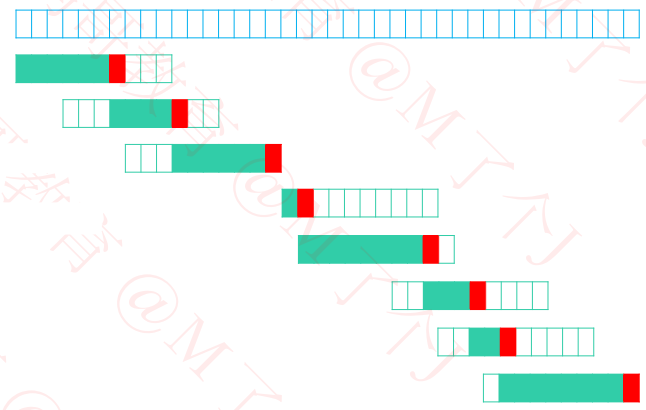
优化效果
KMP - 性能分析
一、性能分析
KMP 主逻辑
最好时间复杂度:O(m)
最坏时间复杂度:O(n),不超过O(2n)
next 表的构造过程跟 KMP 主体逻辑类似
时间复杂度:O(m)
KMP 整体
最好时间复杂度:O(m)
最坏时间复杂度:O(n + m)
空间复杂度: O(m)
二、蛮力算法为何低效?
当字符失配时
蛮力算法
✓ ti 回溯到左边位置
✓ pi 回溯到 0
KMP 算法
✓ ti 不必回溯
✓ pi 不一定要回溯到 0
行者常至,为者常成!
