【进阶】3、排序（三）

2014-03-03 | 阅读：

归并排序（Merge Sort）

1945年由约翰·冯·诺伊曼（John von Neumann）首次提出

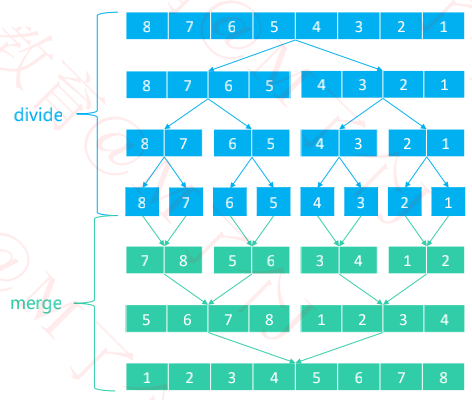
执行流程

divide
① 不断地将当前序列平均分割成2个子序列
✓ 直到不能再分割（序列中只剩1个元素）

merge
② 不断地将2个子序列合并成一个有序序列
✓ 直到最终只剩下1个有序序列

归并排序原理

一、divide实现

-(void)sort{
    [self sortWithBegin:0 end:(int)self.array.count];
}


/// 归并排序divide实现 [begin end) 左闭右开
/// @param begin 起始索引
/// @param end 终止索引
-(void)sortWithBegin:(int)begin end:(int)end{
    //至少要2个元素
    if(end - begin <2) return;
    int mid = (begin+end)>>1;
    
    //拆分左半部分
    [self sortWithBegin:begin end:mid];
    
    //拆分右半部分
    [self sortWithBegin:mid end:end];
    
    //合并左右两部分
    [self mergeWithBegin:begin mid:mid end:end];
}

二、merge

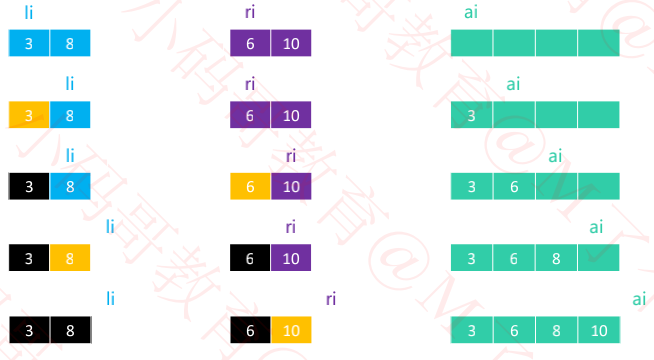
三、merge细节

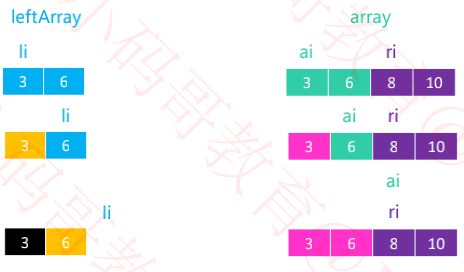
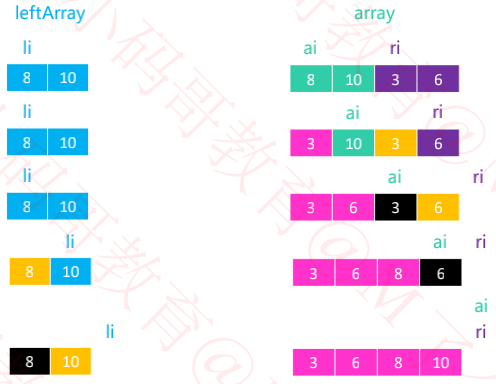
需要 merge 的 2 组序列存在于同一个数组中，并且是挨在一起的

为了更好地完成 merge 操作，最好将其中 1 组序列备份出来，比如 [begin, mid)

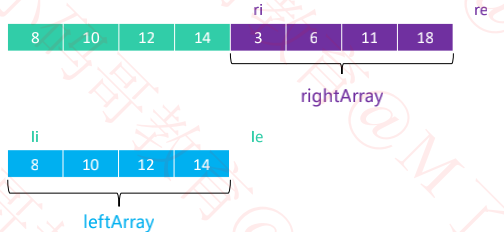
li == 0，le == mid – begin
ri == mid，re == end

merge示例

左边先结束

右边先结束

归并排序实现

//时间复杂度:最好O(nlogn)、最坏O(nlogn)、平均O(nlogn)
//空间复杂度O(n)

-(void)sort{
    [self sortWithBegin:0 end:(int)self.array.count];
}


/// 归并排序divide实现 [begin end) 左闭右开
/// @param begin 起始索引
/// @param end 终止索引
-(void)sortWithBegin:(int)begin end:(int)end{
    //至少要2个元素
    if(end - begin <2) return;
    
    int mid = (begin+end)>>1;
    
    //拆分左半部分
    [self sortWithBegin:begin end:mid];
    
    //拆分右半部分
    [self sortWithBegin:mid end:end];
    
    //合并左右两部分
    [self mergeWithBegin:begin mid:mid end:end];
}



/// 归并排序merge实现 [begin mid) [mid end) 左右两部分
/// @param begin 起始索引
/// @param mid 中间索引
/// @param end 结束索引
-(void)mergeWithBegin:(int)begin mid:(int)mid end:(int)end{
    
    //左边数组索引（备份）
    int li = 0,le = mid - begin;
    
    //右边数组索引（包含在大数组内）
    int ri = mid,re = end;
    
    //当前覆盖索引ai
    int ai = begin;
    
    // 备份左边数组
    for (int i = li; i < le; i++) {
        self.leftArray[i] = self.array[begin + i];
    }
    
    //如果左边没有结束
    while (li<le) {
        if (ri<re && [self compareWithValue1:self.array[ri] value2:self.leftArray[li]]== -1) {
            //右边没有结束 && 右边小于左边
            self.array[ai++] = self.array[ri++];
        }else{
            //右边结束 || 右边大于左边
            self.array[ai++] = self.leftArray[li++];
        }
    }
    
    //左边结束，直接结束
    
}

复杂度分析

一、归并排序所花费的时间

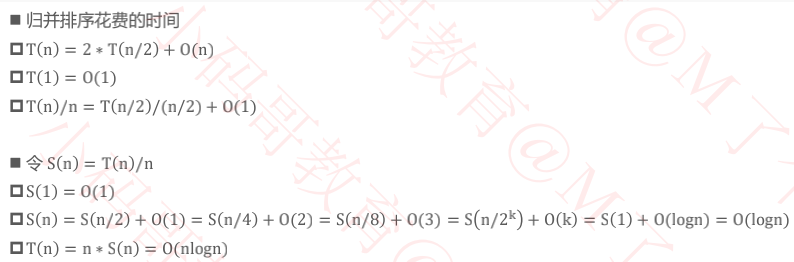
由于归并排序总是平均分割子序列，所以最好、最坏、平均时间复杂度都是 O(nlogn) ，属于稳定排序
从代码中不难看出：归并排序的空间复杂度是 O n/2 + logn = O(n)
n/2 用于临时存放左侧数组，logn 是因为递归调用

二、常见的递推式与复杂度

行者常至，为者常成！

JHHK