目录
快速排序(Quick Sort)
快速排序(Quick Sort)
1960年由查尔斯·安东尼·理查德·霍尔(Charles Antony Richard Hoare,缩写为C. A. R. Hoare)提出
昵称为东尼·霍尔(Tony Hoare)
一、快速排序 – 执行流程
① 从序列中选择一个轴点元素(pivot)
✓ 假设每次选择 0 位置的元素为轴点元素
② 利用 pivot 将序列分割成 2 个子序列
✓ 将小于 pivot 的元素放在pivot前面(左侧)
✓ 将大于 pivot 的元素放在pivot后面(右侧)
✓ 等于pivot的元素放哪边都可以
③ 对子序列进行 ① ② 操作
✓ 直到不能再分割(子序列中只剩下1个元素)
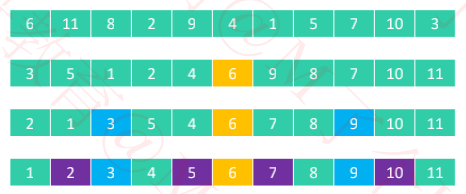
快速排序的本质
逐渐将每一个元素都转换成轴点元素
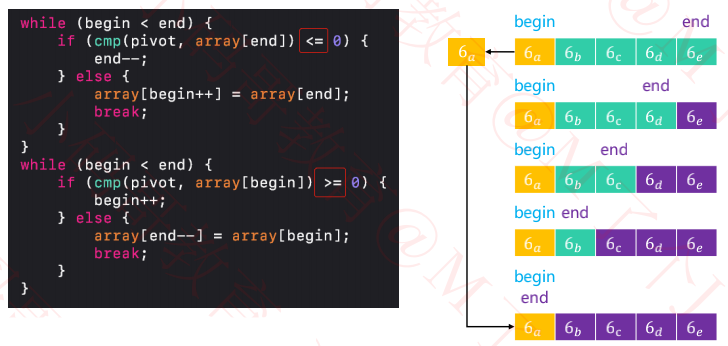
二、快速排序的轴点构造
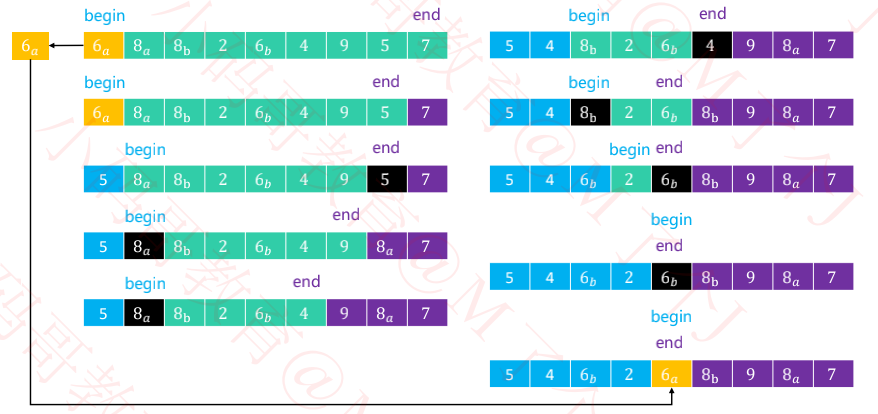
三、快速排序的时间复杂度
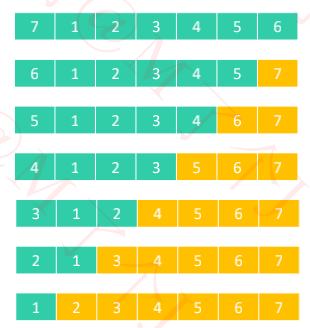
在轴点左右元素数量比较均匀的情况下,同时也是最好的情况
T n = 2 ∗ T n/2 + O n = O(nlogn)
如果轴点左右元素数量极度不均匀,最坏情况
T n = T n − 1 + O n = O(n2)
为了降低最坏情况的出现概率,一般采取的做法是
随机选择轴点元素
最好、平均时间复杂度:O(nlogn)
最坏时间复杂度:O(n2)
由于递归调用的缘故,空间复杂度:O(logn)
属于不稳定排序
四、快速排序的实现
/**
最好、平均时间复杂度:O(nlogn) 最坏时间复杂度:O(n2)
由于递归调用的缘故,空间复杂度:O(logn)
*/
-(void)sort{
[self sortWithBegin:0 end:(int)self.array.count];
}
/// 快速排序[beigin end)
/// @param begin 起始index
/// @param end 结束index
-(void)sortWithBegin:(int)begin end:(int)end{
//至少需要两个元素
if(end - begin<2) return;
//找到轴点元素的位置
int mid = [self pivotIndexWithBegin:begin end:end];
//对左半部分进行快速排序
[self sortWithBegin:begin end:mid];
//对有半部分进行快速排序
[self sortWithBegin:mid+1 end:end];
}
/// 返回轴点元素索引[begin end)
/// @param begin 起始索引
/// @param end 终止索引
-(int)pivotIndexWithBegin:(int)begin end:(int)end{
//为了降低最坏情况的出现概率,一般采取的做法是 随机选择轴点元素
int randomIndex = begin+ random()%(end - begin);//[begin end)
[self swapWithIndex1:begin index2:randomIndex];
//备份pivot元素
id pivot = self.array[begin];
//因为是左闭右开所以end--;
end--;
//当begin = end时,结束
while (begin<end) {
while(begin<end){
//末尾元素大于pivot,end-- 思考:可以将条件改为 <=0 吗? 不可以
if ([self compareWithValue1:pivot value2:self.array[end]] < 0) {
end--;
//末尾元素小于等于pivot,进行交换 begin++
}else{
//self.array[begin] = self.array[end];
[self moveWithFromIndex:end toIndex:begin];
begin++;
//结束,进入轮换
break;
}
}
while(begin<end){
//起始元素小于末尾元素,begin++ 思考:可以将条件改为 >=0 吗? 不可以
if ([self compareWithValue1:pivot value2:self.array[begin]] > 0) {
begin++;
//起始元素大于等于末尾元素,进行交换,end--
}else{
//self.array[end] = self.array[begin];
[self moveWithFromIndex:begin toIndex:end];
end--;
//结束,进入轮换
break;
}
}
}
//放置轴点元素
self.array[begin] = pivot;
//执行到此处begin == end 返回begin或end都可以。该位置就是pivot的索引
return begin;
}
五、快速排序与轴点相等的元素
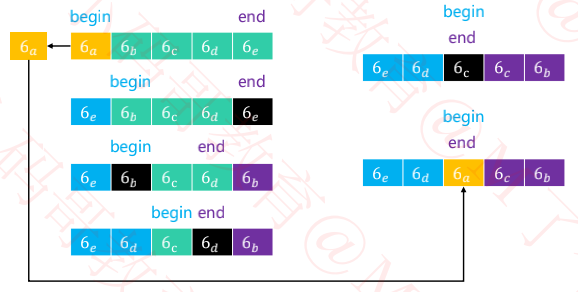
如果序列中的所有元素都与轴点元素相等,利用目前的算法实现,轴点元素可以将序列分割成 2 个均匀的子序列
思考:cmp 位置的判断分别改为 ≤、≥ 会起到什么效果?
轴点元素分割出来的子序列极度不均匀
导致出现最坏时间复杂度 O(n2)
希尔排序(Shell Sort)
一、希尔排序
1959年由唐纳德·希尔(Donald Shell)提出
希尔排序把序列看作是一个矩阵,分成 𝑚 列,逐列进行排序
从某个整数逐渐减为1
当 𝑚 为1时,整个序列将完全有序
因此,希尔排序也被称为递减增量排序(Diminishing Increment Sort)
矩阵的列数取决于步长序列(step sequence)
✓ 比如,如果步长序列为{1,5,19,41,109,…},就代表依次分成109列、41列、19列、5列、1列进行排序
✓ 不同的步长序列,执行效率也不同
二、希尔排序示例一
希尔本人给出的步长序列是 𝑛/2^𝑘,比如 𝑛 为16时,步长序列是{1, 2, 4, 8}

分成8列进行排序
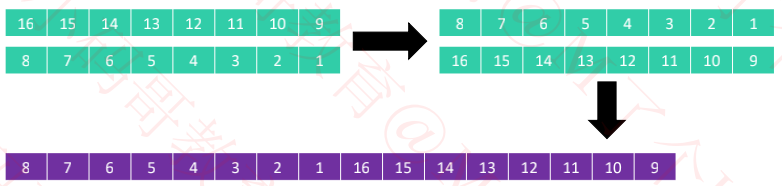
分成4列进行排序
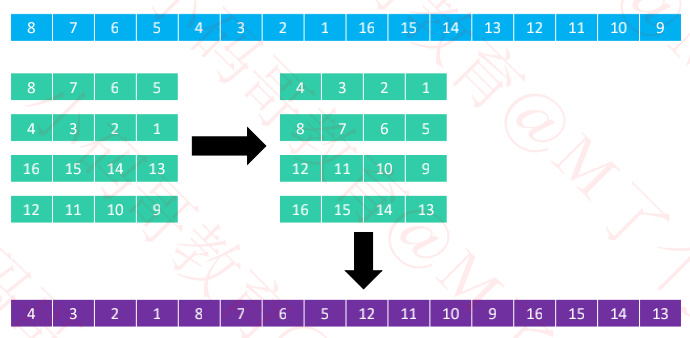
分成2列进行排序
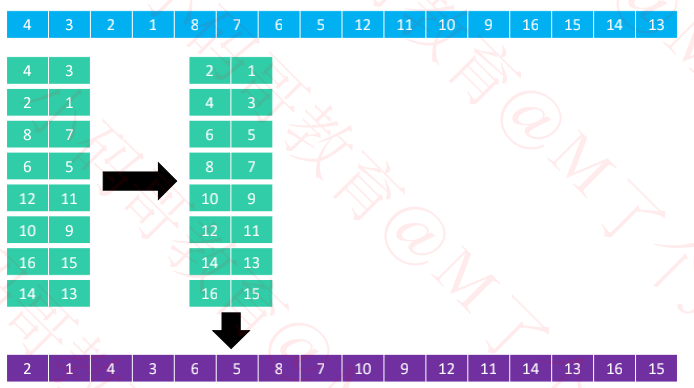
分成1列进行排序
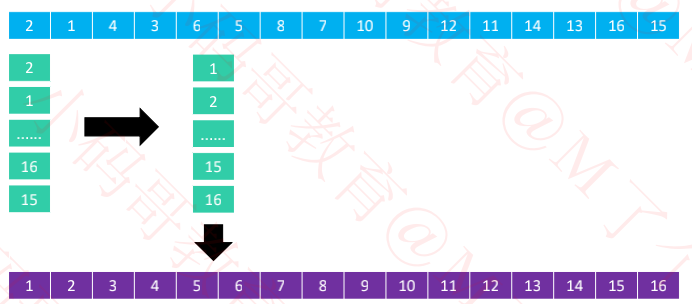
不难看出来,从8列 变为 1列的过程中,逆序对的数量在逐渐减少
因此希尔排序底层一般使用插入排序对每一列进行排序,也很多资料认为希尔排序是插入排序的改进版
三、希尔排序示例二
假设有11个元素,步长序列是{1, 2, 5}
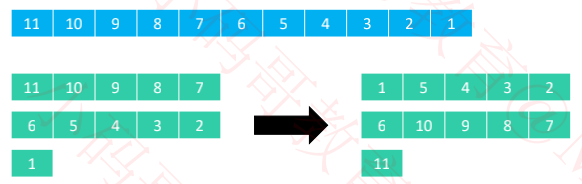
假设元素在第 col 列、第 row 行,步长(总列数)是 step
✅ 那么这个元素在数组中的索引是 col + row * step
✅ 比如 9 在排序前是第 2 列、第 0 行,那么它排序前的索引是 2 + 0 * 5 = 2
✅ 比如 4 在排序前是第 2 列、第 1 行,那么它排序前的索引是 2 + 1 * 5 = 7
四、希尔排序实现
-(void)sort{
NSArray * stepSequence = [self shellStepSequence];
for (int i = 0; i<stepSequence.count; i++) {
[self sortWithStep: [stepSequence[i] intValue]];
}
}
/// 按步长进行排序
/// @param step 步长
-(void)sortWithStep:(int)step{
for (int col = 0; col<step; col++) {
//希尔排序是基于插入排序的
//col col+step col+2*step ...
for (int begin = col+step; begin<self.array.count; begin+=step) {
int current = begin;
while(current>col &&[self compareWithIndex1:current index2:current-step]<0){
[self swapWithIndex1:current index2:current-step];
current-=step;
}
}
}
}
/// 获取希尔步长序列
-(NSArray*)shellStepSequence{
NSMutableArray * array = [NSMutableArray array];
int stepSequence = (int)self.array.count;
while ((stepSequence>>=1)>0 ) {
[array addObject:@(stepSequence)];
}
return array;
}
最好情况是步长序列只有1,且序列几乎有序,时间复杂度为 O(n)
空间复杂度为O(1),属于不稳定排序
五、希尔排序步长
希尔本人给出的步长序列,最坏情况时间复杂度是 O(n2)
目前已知的最好的步长序列,最坏情况时间复杂度是 O(n^(4/3)) ,1986年由Robert Sedgewick提出
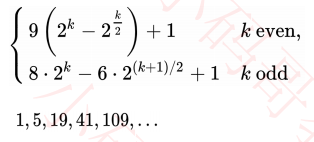
/// Robert Sedgewick 提出
-(NSArray*)sedgewickStepSequence{
NSMutableArray * array = [NSMutableArray array];
int k = 0,step = 0;
while (true) {
if (k%2 == 0) {
int pow0 = pow(2, k >> 1);//计算以x为底数的y次幂
step = 1+9*(pow0*pow0-pow0);
}else{
int pow1 = pow(2,(k-1)>>1);
int pow2 = pow(2,(k+1)>>1);
step = 1 + 8 * pow1 * pow2 - 6 * pow2;
}
if (step>=self.array.count) {
break;
}
[array insertObject:@(step) atIndex:0];
k++;
}
return array;
}
行者常至,为者常成!
