目录
计数排序(Counting Sort)
一、计数排序
之前学习的冒泡、选择、插入、归并、快速、希尔、堆排序,都是基于比较的排序
平均时间复杂度目前最低是 O(nlogn)
计数排序、桶排序、基数排序,都不是基于比较的排序
它们是典型的用空间换时间,在某些时候,平均时间复杂度可以比 O nlogn 更低
计数排序于1954年由Harold H. Seward提出,适合对一定范围内的整数进行排序
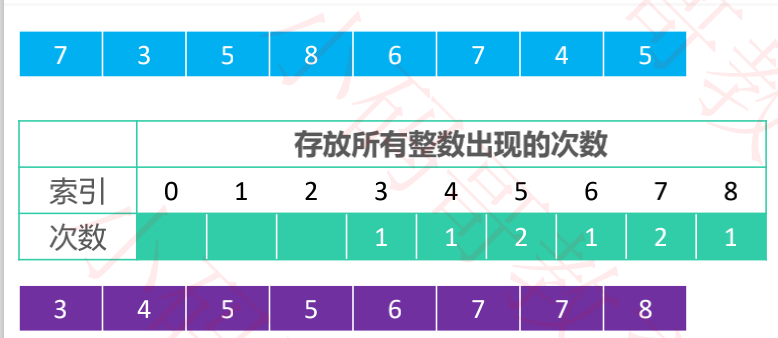
计数排序的核心思想
统计每个整数在序列中出现的次数,进而推导出每个整数在有序序列中的索引
二、最简单的计数排序
-(void)sort{
//找出最大值
int max = [self.array[0] intValue];
for (int i = 0; i<self.array.count; i++) {
if (max<[self.array[i] intValue]) {
max = [self.array[i] intValue];
}
}
//创建一个数组存放元素出现的次数
NSMutableArray * counts = [NSMutableArray arrayWithCapacity:max+1];
for (int i = 0; i<max+1; i++) {
counts[i] = @(0);
}
//统计元素出现的次数
for (int i = 0; i<self.array.count; i++) {
int count = [counts[[self.array[i] intValue]] intValue];
counts[[self.array[i] intValue]] = @(++count);
}
//按顺序赋值
int index = 0;
for (int i = 0; i<counts.count; i++) {
int count = [counts[i] intValue];
while (count-->0) {
self.array[index] = @(i);
index++;
}
}
}
这个版本的实现存在以下问题
无法对负整数进行排序
极其浪费内存空间
是个不稳定的排序
……
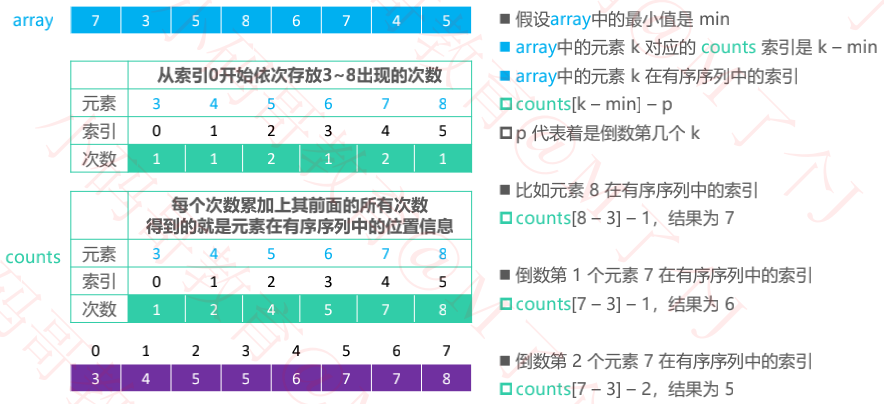
三、计数排序改进思路
//计数排序的改进
-(void)sort{
//找出最大值 最小值
int max = [self.array[0] intValue];
int min = [self.array[0] intValue];
for (int i = 0; i<self.array.count; i++) {
if (max<[self.array[i] intValue]) {
max = [self.array[i] intValue];
}
if (min>[self.array[i] intValue]) {
min = [self.array[i] intValue];
}
}
//创建一个数组存放元素出现的次数
NSMutableArray * counts = [NSMutableArray arrayWithCapacity:max-min+1];
for (int i = 0; i<max-min+1; i++) {
counts[i] = @(0);
}
//统计元素出现的次数
for (int i = 0; i<self.array.count; i++) {
int index = [self.array[i] intValue]-min;
int count = [counts[index] intValue];
counts[index] = @(++count);
}
//对次数进行累加
for (int i = 1; i<counts.count; i++) {
int count = [counts[i-1] intValue] + [counts[i] intValue];
counts[i] = @(count);
}
//创建一个新的数组
NSMutableArray * sortArray = [NSMutableArray arrayWithCapacity:self.array.count];
for (int i = 0; i<self.array.count; i++) {
sortArray[i] = @(0);
}
for (int i= (int)self.array.count-1; i>=0; i--) {
int element = [self.array[i] intValue];
//拿到element在counts中的索引
int index = element-min;
//拿到element的个数
int count = [counts[index] intValue];
//拿到在有序数组中的索引
int sortIndex = count-1;
//element放到有序数组中
sortArray[sortIndex] = @(element);
//更新该元素在counts中的个数
counts[index] = @(count-1);
}
//按顺序赋值
for (int i = 0; i<self.array.count; i++) {
self.array[i] = sortArray[i];
}
}
最好、最坏、平均时间复杂度:O(n + k)
空间复杂度:O(n + k)
k 是整数的取值范围
属于稳定排序
四、对自定义对象进行计数排序
如果自定义对象可以提供用以排序的整数类型,依然可以使用计数排序
基数排序(Radix Sort)
一、基数排序
基数排序非常适合用于整数排序(尤其是非负整数),因此本课程只演示对非负整数进行基数排序
执行流程:依次对个位数、十位数、百位数、千位数、万位数…进行排序(从低位到高位)
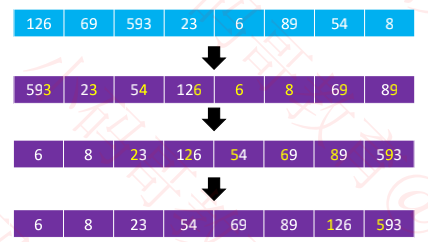
个位数、十位数、百位数的取值范围都是固定的0~9,可以使用计数排序对它们进行排序
思考:如果先对高位排序,再对低位排序,是否可行?
二、基数排序 – 实现
-(void)sort{
//找出最大值
int max = [self.array[0] intValue];
for (int i = 0; i<self.array.count; i++) {
if (max<[self.array[i] intValue]) {
max = [self.array[i] intValue];
}
}
for (int i = 1; i<=max; i*=10) {
[self countingSortWithDivider:i];
}
}
//计数排序的改进
-(void)countingSortWithDivider:(int)divider{
//创建一个数组存放元素出现的次数[0 9]
NSMutableArray * counts = [NSMutableArray arrayWithCapacity:10];
for (int i = 0; i<10; i++) {
counts[i] = @(0);
}
//统计元素出现的次数
for (int i = 0; i<self.array.count; i++) {
int index = [self.array[i] intValue] / divider % 10;
int count = [counts[index] intValue];
counts[index] = @(++count);
}
//对次数进行累加
for (int i = 1; i<counts.count; i++) {
int count = [counts[i-1] intValue] + [counts[i] intValue];
counts[i] = @(count);
}
//创建一个新的数组
NSMutableArray * sortArray = [NSMutableArray arrayWithCapacity:self.array.count];
for (int i = 0; i<self.array.count; i++) {
sortArray[i] = @(0);
}
for (int i= (int)self.array.count-1; i>=0; i--) {
int element = [self.array[i] intValue];
//拿到element在counts中的索引
int index = element / divider % 10;
//拿到element的个数
int count = [counts[index] intValue];
//拿到在有序数组中的索引
int sortIndex = count-1;
//element放到有序数组中
sortArray[sortIndex] = @(element);
//更新该元素在counts中的个数
counts[index] = @(count-1);
}
//按顺序赋值
for (int i = 0; i<self.array.count; i++) {
self.array[i] = sortArray[i];
}
}
最好、最坏、平均时间复杂度:O(d ∗ (n + k)) ,d 是最大值的位数,k 是进制。
属于稳定排序
空间复杂度:O(n + k),k 是进制
桶排序(Bucket Sort)
执行流程
① 创建一定数量的桶(比如用数组、链表作为桶)
② 按照一定的规则(不同类型的数据,规则不同),将序列中的元素均匀分配到对应的桶
③ 分别对每个桶进行单独排序
④ 将所有非空桶的元素合并成有序序列
元素在桶中的索引
元素值 * 元素数量
行者常至,为者常成!
